Geometría básica -
Suma de ángulos
Geometría básica
Suma de ángulos
search
menu
/es/geometria-basica/el-sistema-sexagesimal/content/
La suma de los ángulos y es el ángulo cuya medida es igual a la suma de las medidas de y Estas operaciones pueden ser calculadas de dos maneras: gráfica y numéricamente.
Para sumar dos ángulos gráficamente puedes realizar el siguiente procedimiento:
Ubica el segundo ángulo haciendo que su vértice (su punto de origen) coincida con el del primer ángulo. También deben coincidir los lados de los ángulos.
El ángulo suma será el conformado por las aberturas de los dos ángulos.
En el siguiente interactivo puedes mover los puntos y para variar la medida los ángulos y . En la parte inferior podrás observar cómo se conforma la suma de estos dos ángulos:
Para sumar numéricamente dos ángulos debemos tener en cuenta si las partes de ángulo se están notando en el sistema decimal o sexagesimal. En el caso decimal la suma se realiza de la manera convencional, en el caso sexagesimal se procede así:
Sumemos por ejemplo los ángulos y
Puedes imaginar columnas verticales así: la primera columna es de los segundos, la segunda de los minutos y la tercera de grados.
Por esta razón realizamos la operación y sobran . Esto quiere decir que segundos son dos minutos y cuarenta segundos. Se ponen los cuarenta segundos en la columna de los segundos y los dos minutos pasan como acarreo a la columna de los minutos.
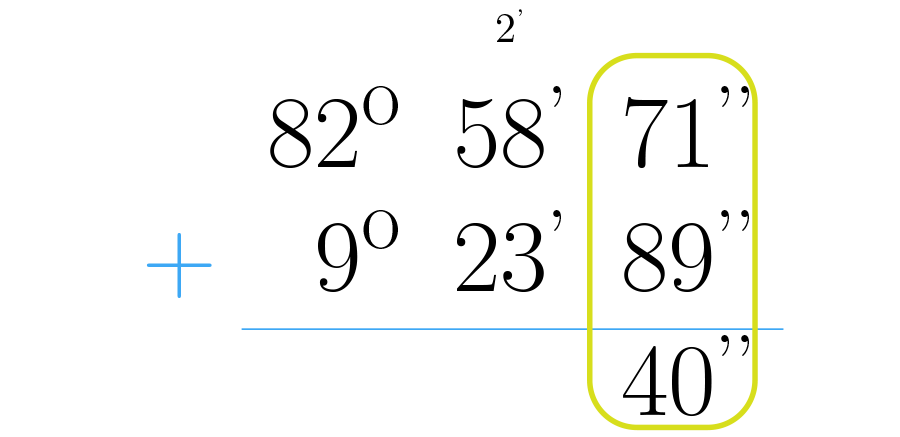
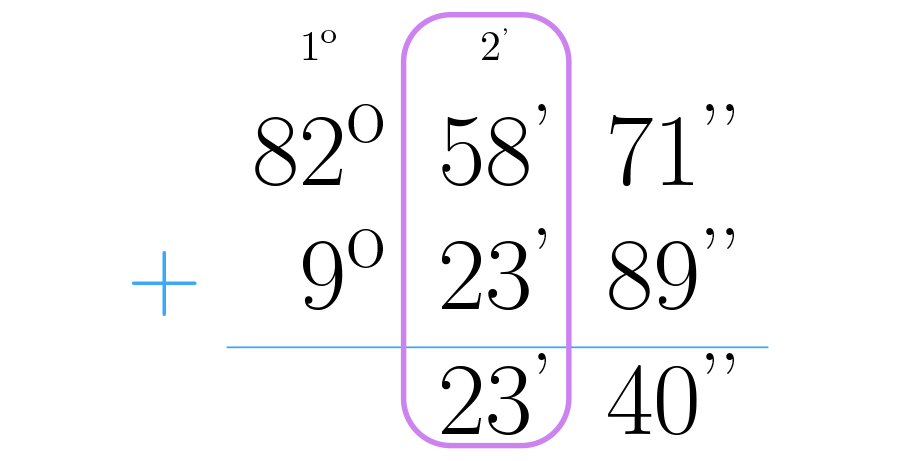
Como los segundos, los minutos se cuentan hasta , se debe entonces saber cuántos grupos de se pueden hacer con minutos. Se realiza la operación , que da como resultado y sobran . Esto quiere decir que minutos son un grado y minutos más.
Se ubican los minutos en la casilla de los minutos y se pasa el grado como acarreo a la columna de los grados.
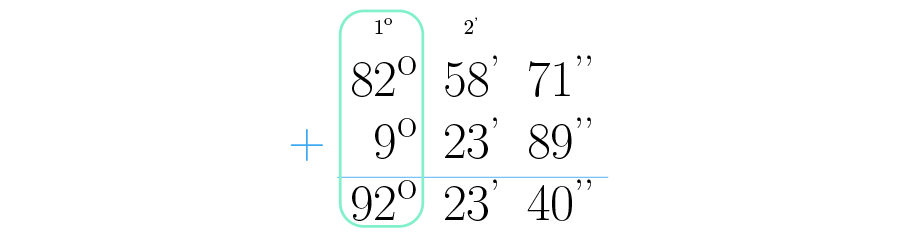
Finalmente se realiza la operación que da como resultado . Así, se ha obtenido el resultado total: .
/es/geometria-basica/resta-de-angulos/content/
