/es/los-decimales/decimales-exactos-a-fraccion/content/

Decimales periódicos puros a fracción

Los decimales periódicos también se pueden representar a través de fracciones.  Aprende cómo hacerlo aquí:

En esta ocasión aprenderás a encontrar fracciones que representen lo mismo que números como o , cuyas colas decimales no terminan pero se repiten periódicamente.

Para conseguir este objetivo te brindaremos un método sencillo que debes seguir paso a paso.  Observa como ejemplo el número

Paso 1: Reescribe el número

Escribe el número con la notación resumida de la barra en la cola decimal.  En este caso en lugar de escribir se escribe:  .

Paso 2: El numerador

El numerador de la fracción será el número decimal escrito sin coma y sin barra, menos la parte entera del mismo, en este caso:

Paso 3: El denominador

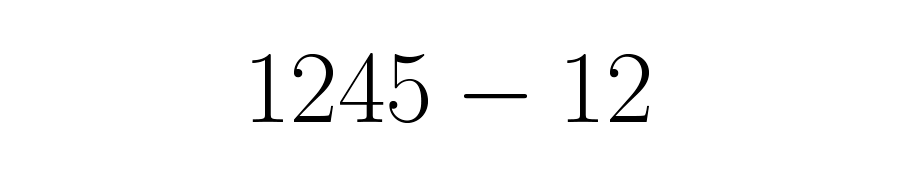
El denominador será un número con tantos nueves como cifras decimales tenga el número original en su notación de barra.  

Como tiene dos cifras periódicas en su cola decimal, el y el , se deben poner dos nueves como denominador.  Recuerda que en este paso siempre se usa el número .

Paso 4: Realizar las operaciones

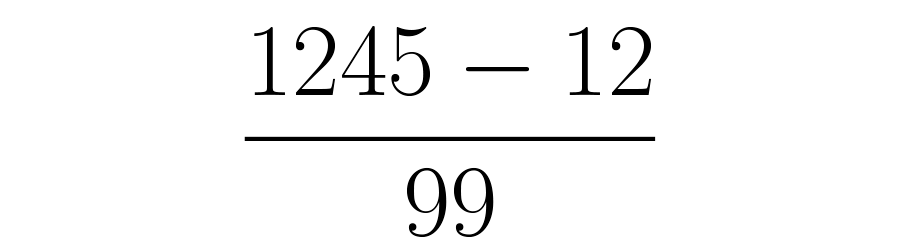
Ahora se resta y simplifica: en esta ocasión se debe realizar la resta: , obteniendo la fracción .  Al simplificar esta misma da como resultado .

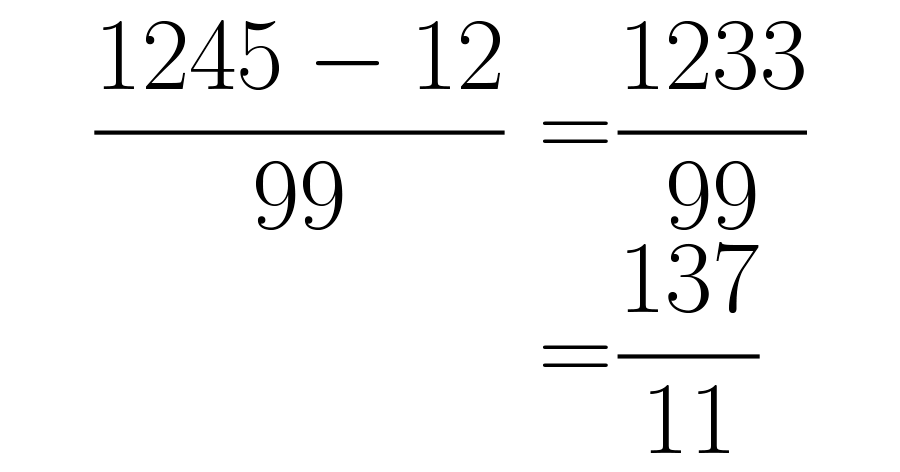
Si realizas la división , encontrarás que su resultado es   Lo anterior quiere decir que .

Otro ejemplo

Observa un ejemplo más interesante: encontremos una fracción que represente el decimal

Paso 1:

Se escribe el número con la notación de barra:

Paso 2:

El numerador será el número escrito sin coma y sin barra, menos la parte entera del mismo número.  Recuerda que

Paso 3. 

El denominador será tantos nueves como cifras decimales periódicas tenga el número original.  En este caso hay solamente una cifra decimal periódica, por lo tanto el denominador tendrá un solo nueve.

Paso 4:

Para finalizar se realiza la resta y se simplifica.  Al simplificar la fracción se obtiene como resultado .

Observa el procedimiento completo en la siguiente imagen:

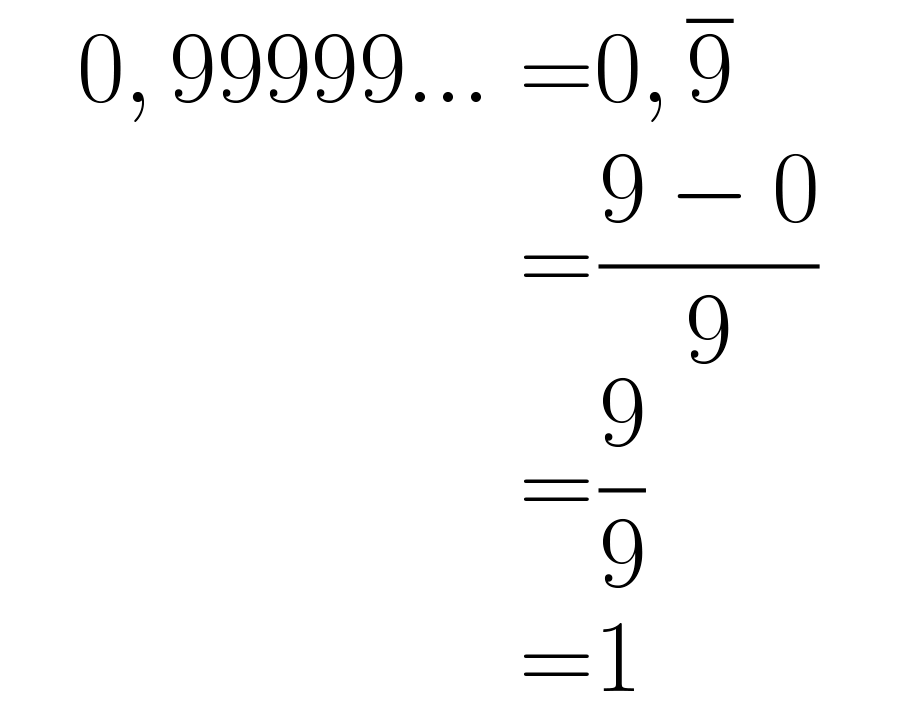
Lo anterior quiere decir que .  ¿No te parece sorprendente que un cero seguido por infinitos nueves sea lo mismo que ?

Piénsalo de la siguiente manera:  si dos números son distintos es posible poner otros números entre ellos.  Por ejemplo, entre y es posible ubicar el   y muchos otros, pero ¿qué número puede haber entre y ?

Para ubicar el hay que tomar nueve décimas, nueve centésimas, nueve milésimas, nueve diezmilésimas, etc., etc., etc.  Y cada vez estarías más y más cerca de la posición que ocupa el uno.  Esto quiere decir que no se puede poner ningún número entre y   Por lo tanto: .

/es/los-decimales/decimales-periodicos-mixtos-a-fraccion/content/