Los decimales: Relación de orden con números decimales

Página 5: Relación de orden con números decimales

/es/los-decimales/clasificacion-de-los-decimales/content/

Relación de orden con números decimales

Establecer relaciones de orden entre los números es determinar cuál de ellos es mayor y cuál menor. Ya sabes como establecer relaciones de orden entre números naturales, enteros y racionales, ahora aprenderás como hacerlo con decimales.

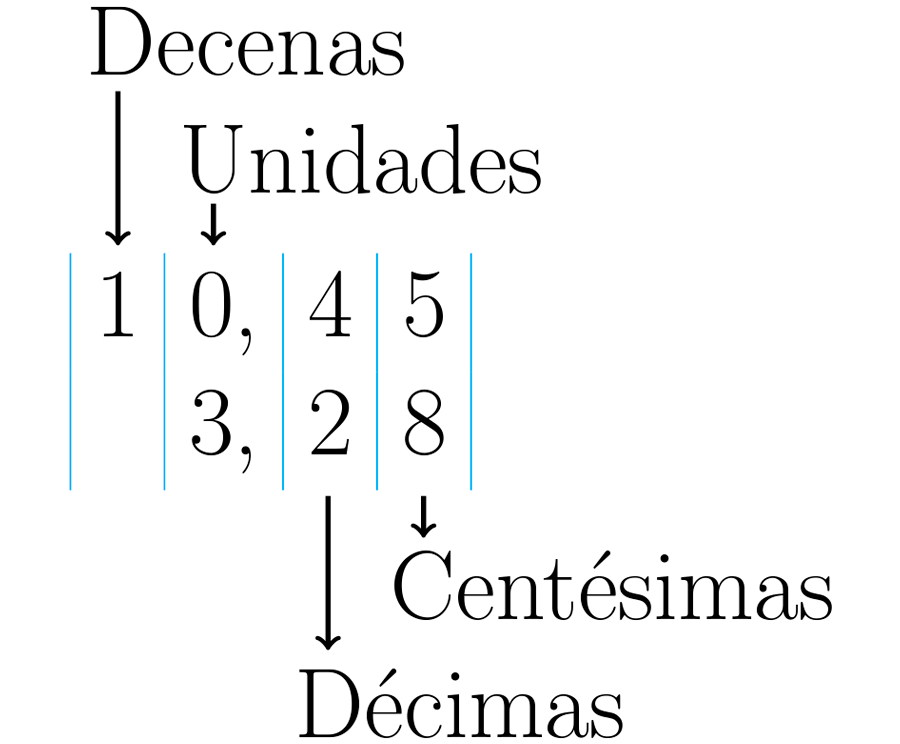
Primero se tienen en cuenta los valores posicionales enteros, es decir, las unidades, decenas, centenas, etc. Posteriormente los valores posicionales decimales: las décimas, centésimas, milésimas, etc. Tomemos como ejemplo los números y :

Se comienza comparando cada valor posicional de izquierda a derecha. Esto quiere decir que se le está dando prioridad a los más significativos: los que más unidades representan.

En este caso hay un uno en la posición de las decenas del primer número y cero en las decenas del segundo. Se puede afirmar inmediatamente que el primero es mayor: .

Otro ejemplo

Comparemos los números y .

Nuevamente se empieza de izquierda a derecha. En este caso los dos números comienzan en las unidades: cada uno tiene dos. Como este valor posicional no determinó cual es mayor se continúa con el próximo a la izquierda.

Se comparan ahora las décimas: los dos números tienen tres décimas cada uno. Hasta aquí no se puede decidir cual es mayor, se debe comparar el siguiente valor posicional.

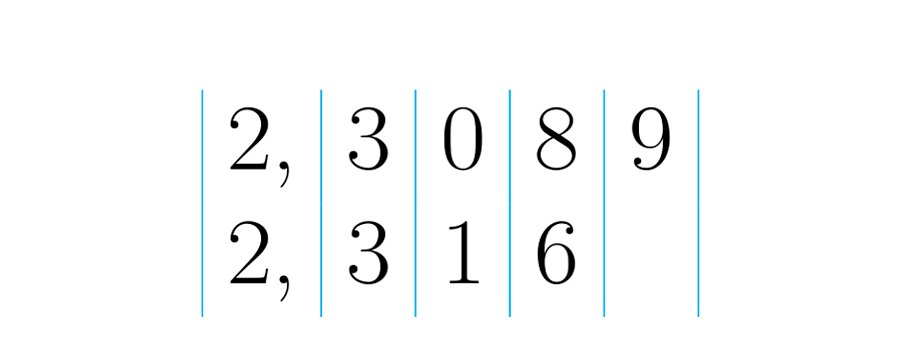
Las centésimas: el primer número tiene cero centésimas, y el segundo una. Podemos entonces afirmar que el segundo número es mayor que el primero: .

Observa que aunque la cola decimal del primer número, , parece mayor que la del segundo, , esto no quiere decir que sea mayor que . No te dejes confundir de estas apariencias.

Comparación de decimales negativos

Cuando se comparan dos números decimales negativos es bueno recordar que el signo menos se interpreta como una deuda. Así, resultará mayor el número que menos deuda represente.

Comparemos los números y : aplicando el método explicado anteriormente te puedes dar cuenta que es mayor que . Así que es una deuda mayor que . Es decir, es menor que .

Observa que al representar estos números en la recta, el menor está a la izquierda del mayor. Esto concuerda con las explicaciones hechas acerca del orden en la recta numérica.