Conceitos básicos da matemática
A Jóia dourada da Matemática


/pt/conceitos-basicos-da-matematica/como-tirar-o-minimo-multiplo-comum-ou-mmc/content/
Você já se perguntou se existe alguma relação entre a natureza e a matemática?
Se você tiver uma fotografia sua ou de alguém, onde é possível ver um rosto de frente, como na imagem abaixo, calcule as medidas e realize as seguintes divisões: , y .
Na grande maioria das pessoas, os resultados desta divisão deve dar mais ou menos 1,6. Fantástico não é verdade?

Não se trata de uma coincidência, a verdade é que nosso corpo possui alguns segredos da matemática. O Universo inteiro está estruturado com princípios matemáticos milenares. Para começar, vamos chamar de proporções todas as divisões iguais as que fizemos acima. No próximo exemplo, vamos calcular a proporção entre e . Para isso, devemos fazer a divisão entre e :
Desta forma dizemos que a proporção entre e é . Isto é o mesmo que dizer que 8 é duas vezes o número . O conceito de proporção nos dá uma ideia de quantas vezes uma quantidade contém outra.
O que acabamos de explicar é a "Versão" aritmética do conceito de proporção. Existe também uma versão geométrica, onde um segmento é uma porção finita de uma reta. Para cada segmento que criamos podemos lhe dar um número em particular, ou seja, uma medida.
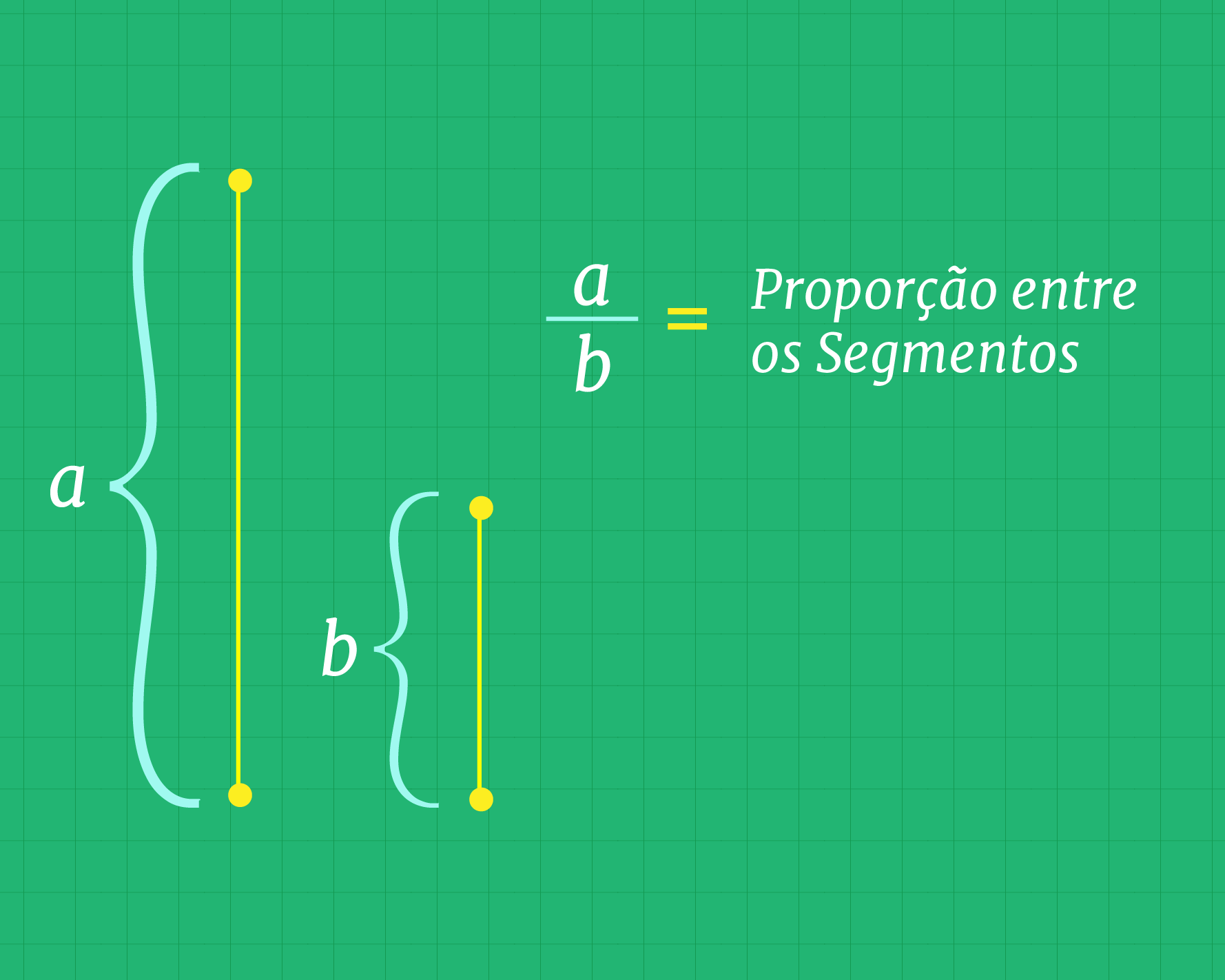
Se criamos dois segmentos de medida e , podemos dizer que a relação existente entre eles deve ser tirada através da divisão das suas medidas, esta divisão é, portanto, a proporção dos segmentos.
Agora vamos criar um segmento com e do seu lado um outro segmento com , é claro que a proporção entre estes dois segmentos é:
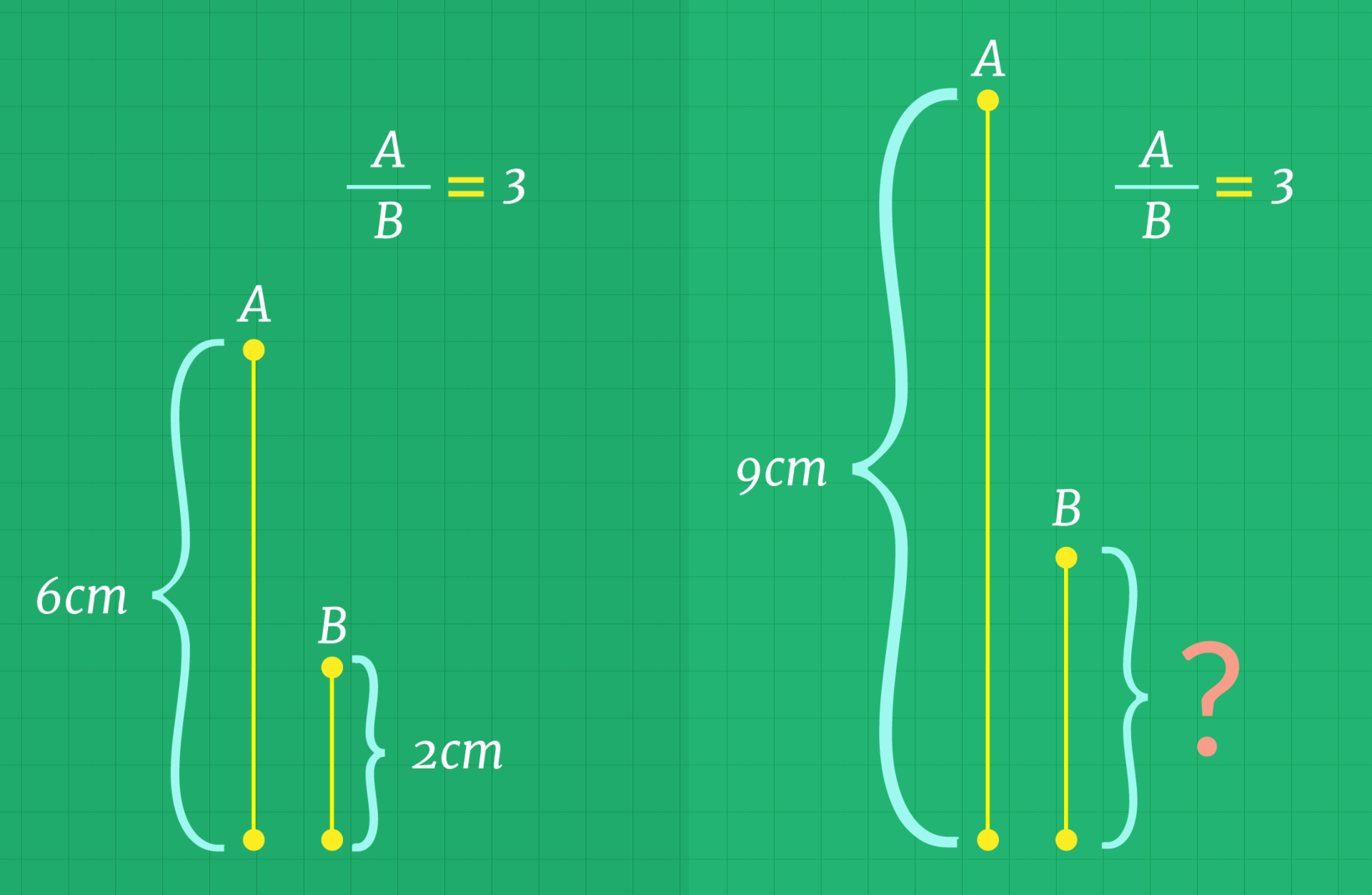
Mas se criamos o segmento de de longitude, com quantos centímetros deveremos criar o segmento para que a proporção entre eles seja ?
Você já deve saber que a resposta é , assim teremos e as proporções entre esses dois pares se manterão iguais:
Usando este simples conceito, você entenderá uma das relações mais interessantes que possui a matemática com o mundo real. Falamos do número Phi (), veja:
Agora, vamos considerar o segmento , conforme nos mostra a figura abaixo. Marcamos um ponto no seu interior, e se você observar, além do segmento agora temos outros dois, o e o . Deste maneira, podemos dizer que + é a longitude total do segmento .
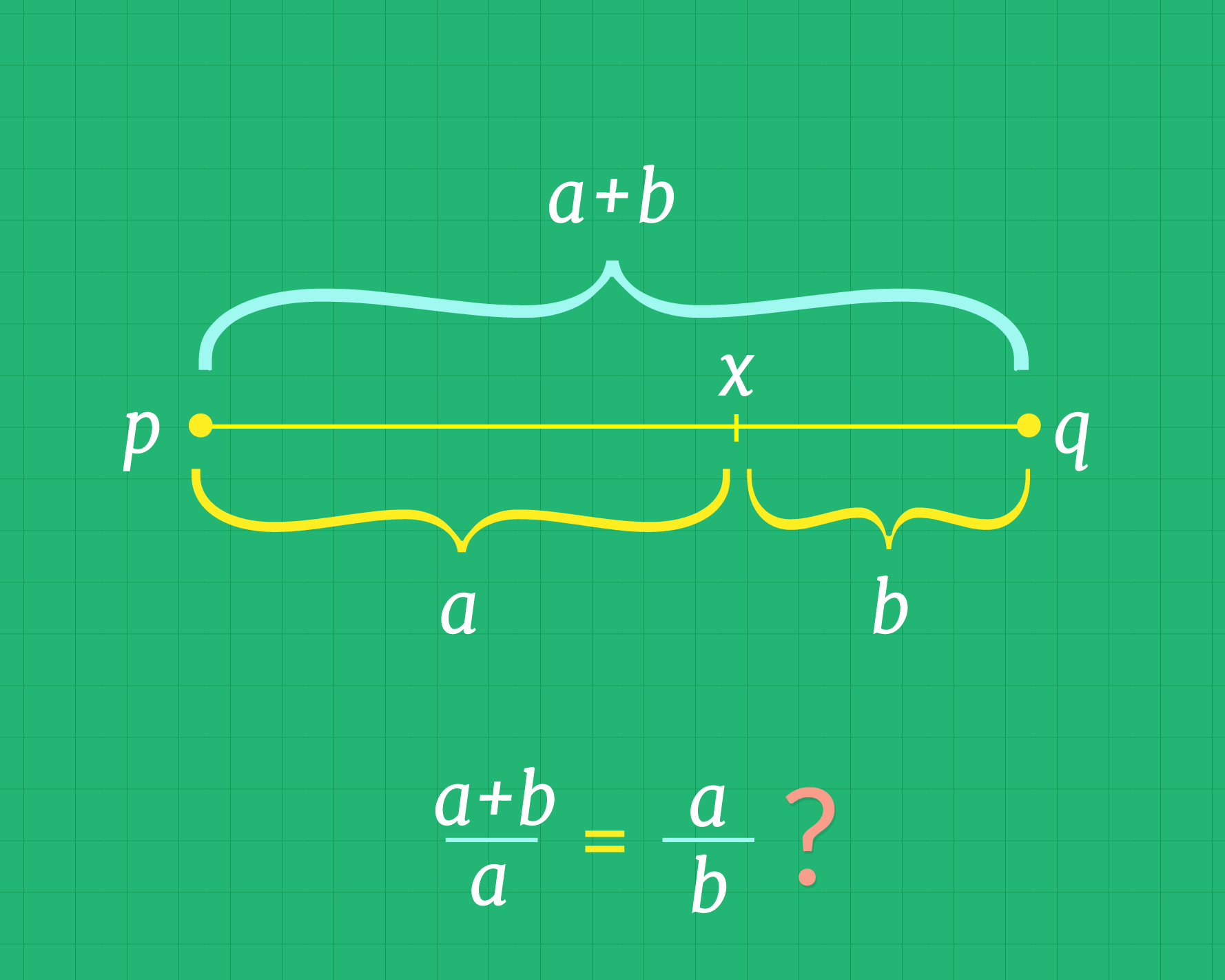
Você acha que é possível escolher o ponto interior , de maneira que as proporções e sejam iguais? Por exemplo, suponhamos que o segmento tenha uma longitude de , se colocamos o ponto na sua metade, os segmentos e medirão cada um. Se calculamos as proporções e obteremos:
e
Como você pode perceber, as proporções e não são iguais. Respondendo a pergunta feita anteriormente, sim é possível pôr o ponto numa determinada posição para que as proporções mencionadas sejam iguais. Mas isto só é possível num determinado ponto do segmento onde as proporções sejam de aproximadamente 1,618... Esta proporção conhecemos como phi (), proporção áurea ou proporção de ouro. Vejamos outras medidas do nosso corpo que também possuem a proporção áurea:
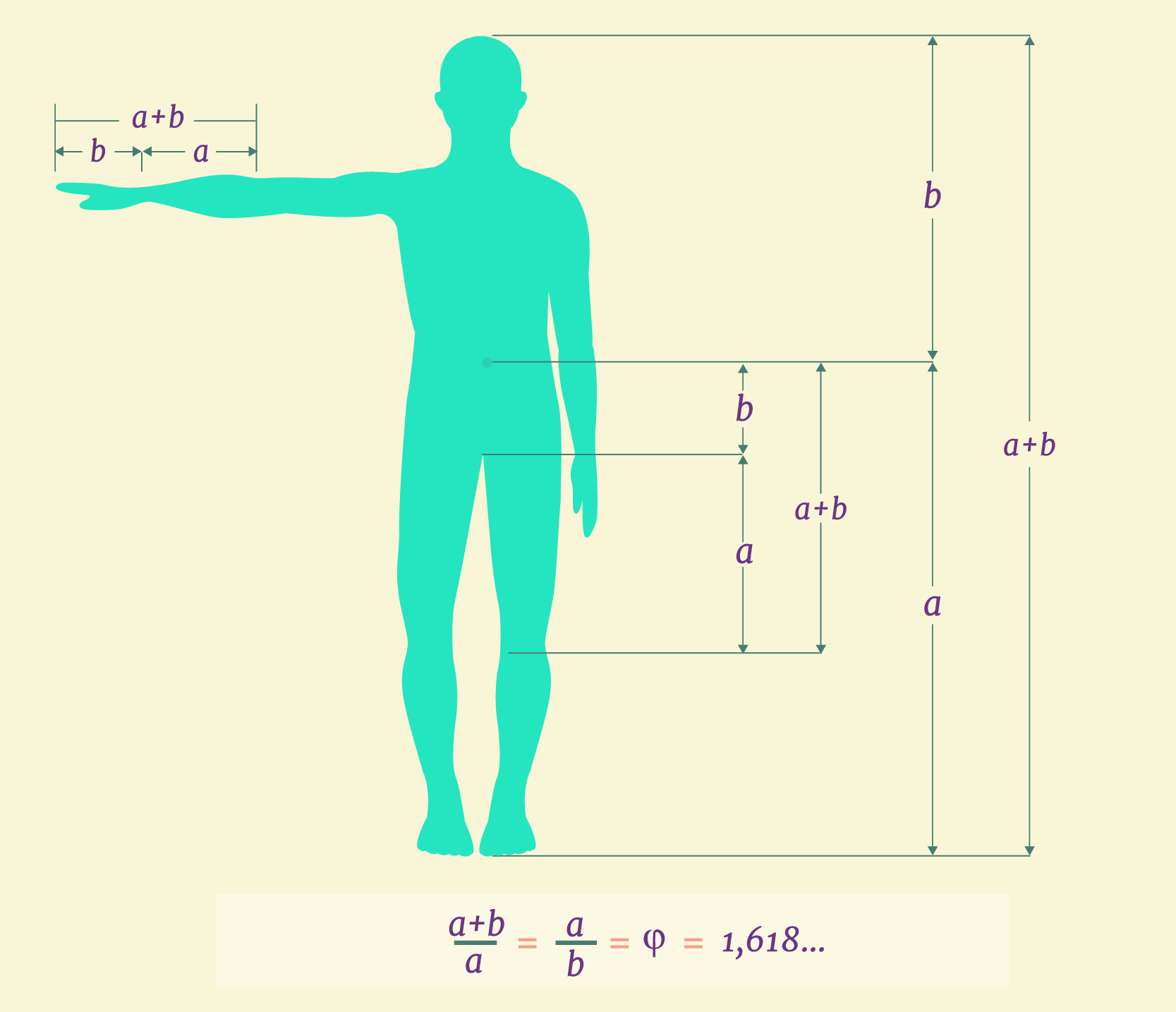
Estes são apenas alguns exemplos de como o está presente no nosso corpo. Mas ele também se manifesta na natureza, e para conferirmos isso precisamos conhecer uma importante figura geométrica que nos permite reconhecer padrões que estão em várias espécies de seres vivos como o náutilo ou na forma de algumas galáxias e ainda no formato dos furacões.
Esta figura é conhecida como espiral áurea e está presente na natureza em formas surpreendentes.
Dada as propriedades do número áureo, não nos espanta saber que muitos o associaram a coisas divinas. Além disso, como podemos ver, vários artistas fizerem uso da proporção dourada para criarem suas obras.
Como você notou, ainda que de forma sutil, a relação entre a matemática e a natureza é fascinante. Aqui apresentamos exemplos simples que servem para mostrar como o () está presente em nossas vidas sem que notemos.
/pt/conceitos-basicos-da-matematica/breve-historia-dos-numeros-i/content/