/pt/multiplos-e-divisores/encontrar-a-decomposicao-prima-de-um-numero/content/
Uma das vantagens de encontrar a decomposição prima de um número é que nos permite saber quantos divisores têm e calculá-los facilmente.
Observe: a decomposição prima de é e se usamos as propriedades associativa e comutativa, podemos encontrar decomposições não primas do número.
Por exemplo, se associamos os três primeiros fatores e os três últimos, obtemos que . Isto permite concluir que e são divisores de :
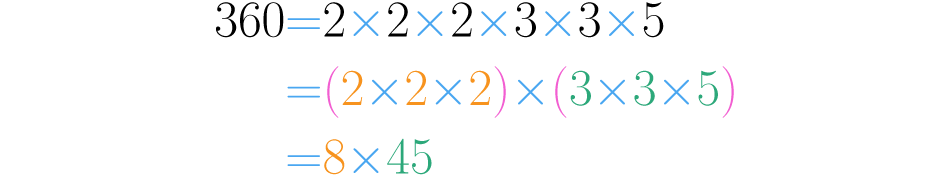
Se comutamos e associamos de outra forma, encontramos outros divisores: onde vemos que e também são divisores de .
Todos os divisores de um número são apresentado quando multiplicamos as diferentes combinações de fatores da sua decomposição prima.
Quando escrevemos a decomposição prima em forma de potências é fácil determinar quantos divisores têm um número. A única coisa que devemos fazer é somar uma unidade para cada expoente e multiplicar os resultados.
Continuando com o exemplo de , se escrevemos sua decomposição em forma de potências obteremos:
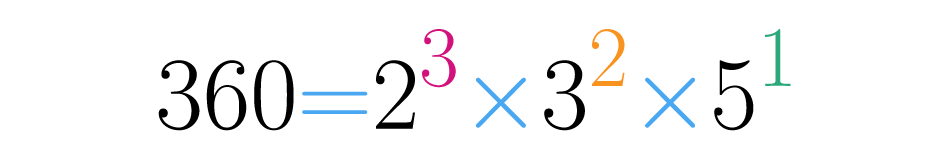
Os expoentes nesta decomposição são , e e quando somamos uma unidade com cada um e multiplicamos os resultados obtemos:
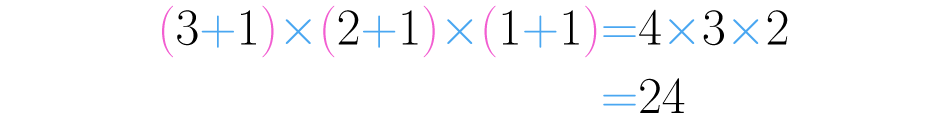
Isso quer dizer que tem divisores.
Já sabemos que para obter os divisores de um número multiplicamos diferentes combinações de seus fatores primos. Contudo, este processo pode ser confuso, porque em algumas ocasiões é fácil esquecer algumas destas combinações. Por isso, veja este método para encontrar tudo sem problemas. Continuamos com o número como exemplo:
Neste caso o primeiro fator primo é Observe que seu expoente é , então as diferentes potências são: , , e .
Fazemos uma fileira com todos os resultados dessas potências:
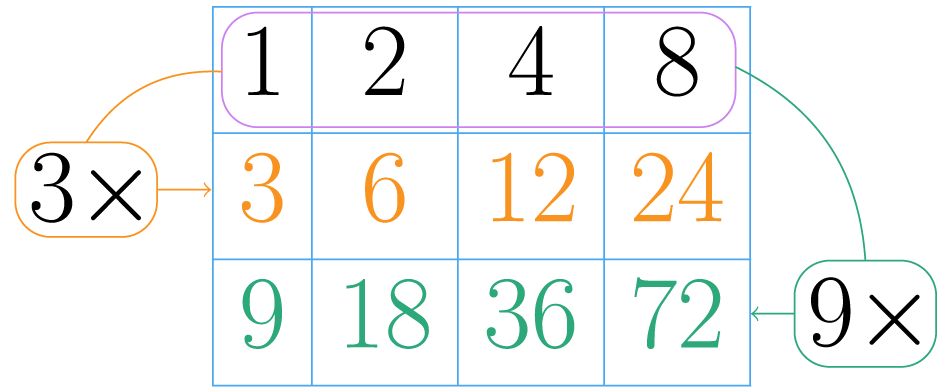
Não é necessário considerar o fator , porque ao multiplicar a primeira fileira por , obtemos a mesma fileira sem alterações.
Agora devemos repetir o passo anterior com todas as potências do terceiro fator. Neste caso o terceiro fator é , e como tem expoente , só multiplicamos as fileiras anteriores por .
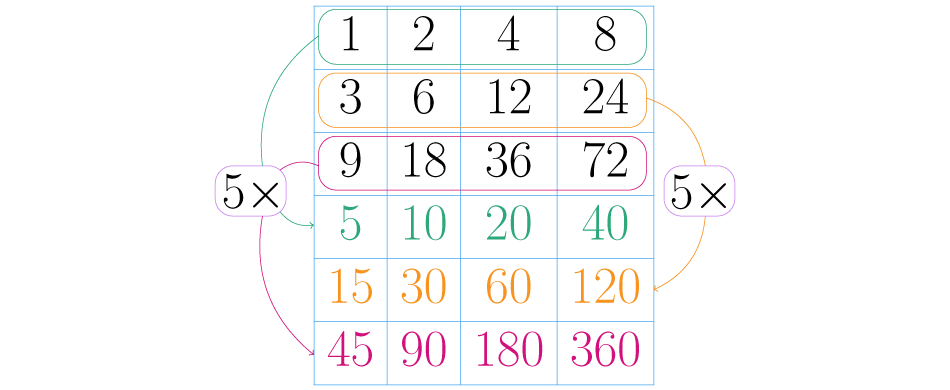
Se o expoente do tivesse sido por exemplo, , teríamos que multiplicar cada fileira também por , e isso produziria três fileiras adicionais.
Como não há mais fatores na decomposição de o processo está terminado. Veja que na tabela temos exatamente números, estes são todos os divisores de .
/pt/multiplos-e-divisores/o-maximo-divisor-comum/content/
