Múltiplos e divisores
Decomposição em fatores primos


/pt/multiplos-e-divisores/os-numeros-primos/content/
Alguns dizem que os números primos são os tijolinhos da matemática. Veja porque:
Para entender o que significa decompor um número em fatores primos, precisamos lembrar do significado da palavra fator: termo que está multiplicando. Por exemplo, na expressão , quatro é o fator de cinco, e cinco é fator de quatro, isto porque cada um está multiplicando o outro. Nada mais simples não é verdade? Agora podemos entender mais profundamente o que significa fatorizar um número.
É possível, por exemplo, representar vinte unidades de várias formas: , ou são algumas delas. Mas podemos escrever em fatores? ou seja, podemos escrever vinte representado como uma multiplicação de números inteiros? Claro: , portanto dizemos que é uma fatoração de . Fatorizar um número é encontrar uma forma de escrevê-lo como multiplicação. Observamos então que os fatores são os divisores do número.
Mas isto só tem sentido para números compostos, porque para números primos a descomposição é trivial. Por exemplo, as únicas fatorações possíveis de são: e .
Como você já pode imaginar, podemos fatorizar (ou decompor) um número de muitas formas diferentes.
Usemos como exemplo o número onde na imagem abaixo podemos observar algumas das formas que podemos decompô-lo.
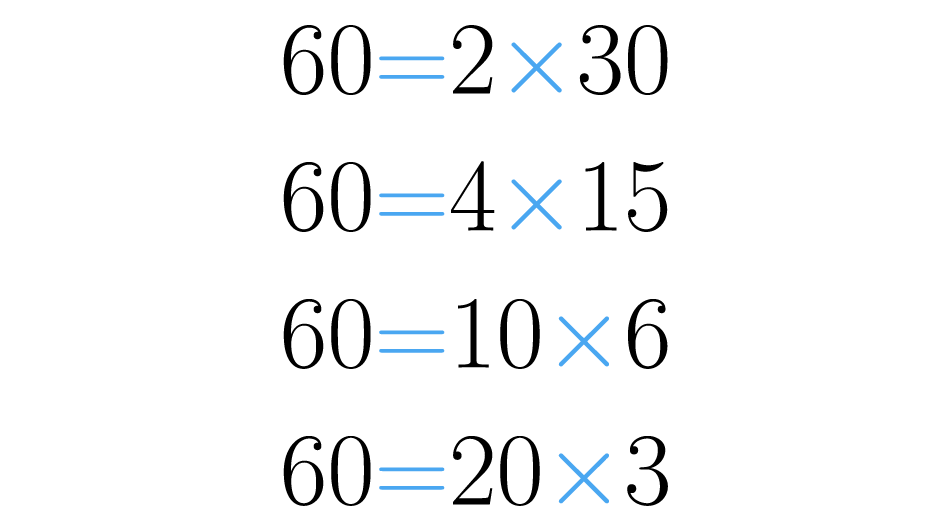
Lembre-se que os números primos são maiores que um e possuem dois divisores: o um, e ele mesmo. Já os compostos têm vários divisores, por isto sempre podemos decompor os números até que cada um dos seus fatores seja primo. Observe:
Vejamos a fatoração do número , por exemplo . Observe que seis e dez são números compostos, porque e .
Isso quer dizer que podemos decompor seis e dez em mais fatores, por exemplo: e . Assim a decomposição de se transforma:
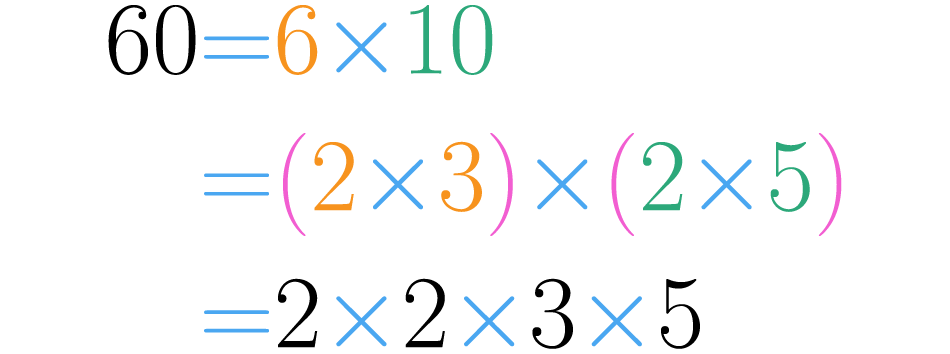
Usando as propriedades comutativa e associativa da multiplicação, podemos escrever a decomposição do menor para o maior e sem parêntesis, como está indicado na imagem anterior.
Agora cada um dos fatores na decomposição de é um número primo, e como estes não tem mais divisores que um e eles mesmos, não é possível seguir transformando, a não ser pela ordem.
Observe que se tivéssemos começado por outra decomposição de , chegaríamos ao mesmo resultado.
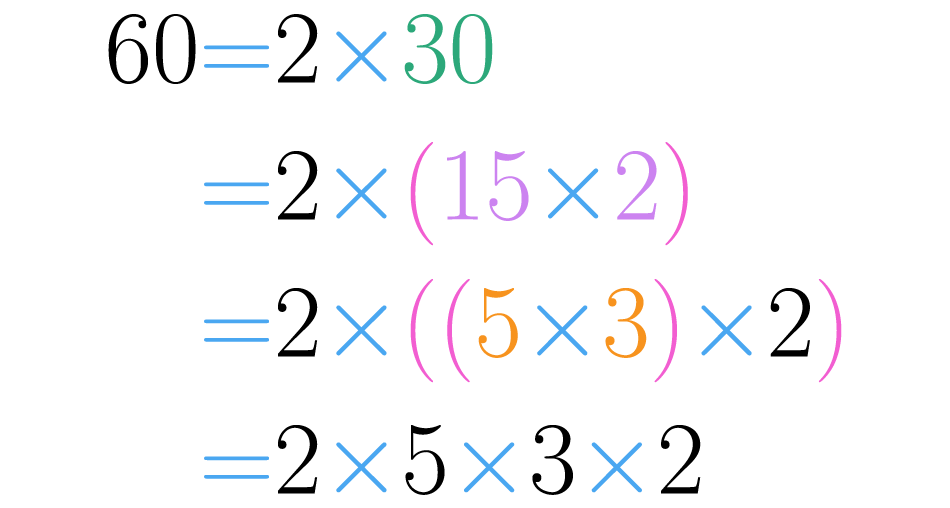
A única diferença entre esta decomposição e a obtida anteriormente, é a ordem dos fatores primos.
A situação anterior vale para todos os números, e significa que todo número natural maior que um, ou é primo ou pode ser escrito como produto de primos. Esta afirmação é uma das mais importantes da matemática e recebe um nome especial: teorema fundamental da aritmética.
Na hora de decompor números em fatores primos podemos encontrar alguns com uma grande quantidade de fatores, um exemplo disso é :
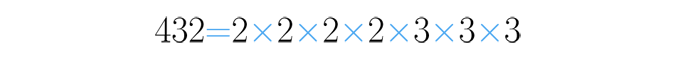
Para simplificar a escrita destas decomposições fazemos o seguinte: só anotamos uma vez cada fator primo, mas escrevemos as vezes que se repete com um pequeno número na parte de cima do lado direito.
Assim, a decomposição de é expressada: , porque o o fator dois aparece quatro vezes e o fator três aparece três. Lemos estes tipos de expressão assim: dois elevado a quatro vezes três elevado a três.
Na expressão percebemos que é o expoente, enquanto o é chamado de base. Na expressão , o é expoente e o é a base. Chamamos esta forma de escrever os produtos de potenciação.
/pt/multiplos-e-divisores/encontrar-a-decomposicao-prima-de-um-numero/content/