Múltiplos e divisores
O máximo divisor comum


/pt/multiplos-e-divisores/a-decomposicao-prima-e-os-divisores/content/
O máximo divisor comum é uma das ferramentas mais importantes da aritmética, aprende aqui a calculá-lo.
Como já tínhamos visto, os números podem compartilhar vários dos seus divisores. Por exemplo, calculamos os divisores de e :
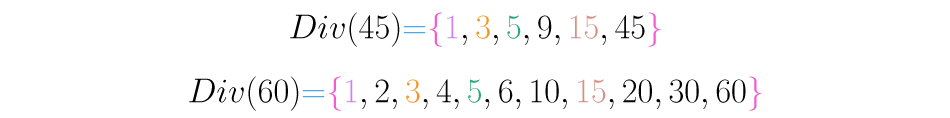
Observe que os números e são os divisores comuns de e . Como veremos mais adiante, o maior destes números, o máximo divisor comum, será muito útil na realização de operações e em suas simplificação, por isso é necessário aprender a calculá-lo.
Uma forma óbvia de calcular o máximo divisor comum de vários números é mostrando todos os divisores dos números em questão, escolher um a um os comuns e depois estabelecer qual é o maior deles. Para o caso de e , percebemos que o máximo divisor comum é .
Este método nem sempre é o mais prático. Você já imaginou calcular o máximo divisor comum de números grandes como e ? Para fazer isso teríamos que encontrar cada um de seus divisores e em seguida observar qual é o maior deles! Este procedimento não é o único, lhe explicaremos um mais simples e rápido. Vejamos como calcular o máximo divisor comum de e :
Primeiro devemos realizar a decomposição prima de cada um dos números:

Percebemos assim que e .
Para calcular o máximo divisor comum multiplicamos os fatores primos que sejam comuns aos números, mas com o menor expoente com que se encontrem.
Neste caso, os fatores primos comuns são e e o menor expoente onde aparecem estes fatores é o um.
Devemos considerar que quando um número aparece sem expoente consideramos que é um. Por exemplo, .
Multiplicamos então , obtendo que o máximo divisor comum de e que é .
Escrevemos o máximo divisor comum dos números e assim: . Podemos escrever então . Vejamos outro exemplo, calculemos o de , e .
Decompomos os números em fatores primos:

Podemos afirmar que , e . Observe que e são os únicos fatores primos comuns a estes três números.
Agora multiplicamos os fatores comuns com o menor expoente que aparece. O menor expoente que aparece com o é um, enquanto que o menor expoente que parece com o é dois, multiplicamos então .
Desta forma percebemos que o máximo divisor comum de , e é , ou seja: .
Quando o de dois números é um, dizemos que são primos relativos, coprimos ou primos entre si. Por exemplo, decompomos os números e :
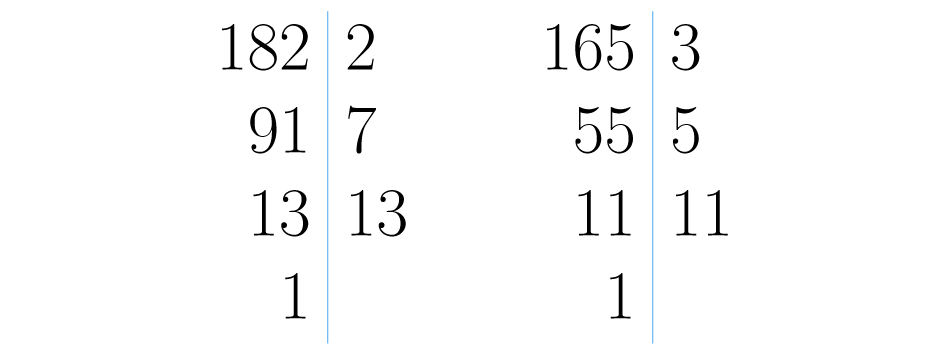
e . Quando não tem fatores primos em comum, quer dizer que não tem divisores comuns mais que , portanto: .
Assim e são primos relativos, coprimos ou primos entre si.
/pt/multiplos-e-divisores/propriedades-dos-divisores/content/