/pt/multiplos-e-divisores/o-que-sao-multiplos/content/
O conceito de mínimo múltiplo comum é fundamental na matemática! Veja o que é e como funciona aqui nesta página.
Para entendermos o conceito de mínimo múltiplo comum, usaremos como exemplo os múltiplos de e , na imagem abaixo é possível observar:
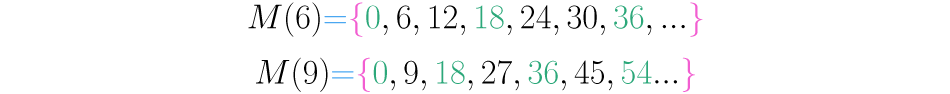
Para encontrar os múltiplos comuns fazemos a intercecção dos conjuntos de múltiplos:
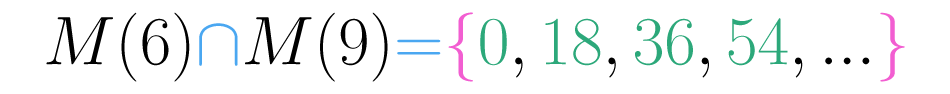
O conjunto de múltiplos comuns de dois (ou mais) números pode ser infinito, por isso não tem sentido pensar que exista um maior de todos eles, ou seja, não existe um máximo múltiplo comum, mas sim podemos encontrar o menor e isso é bastante útil.
Entendemos que mínimo múltiplo comum, , de dois números naturais e é o menor dos múltiplos comuns entre e que é diferente de zero. Escrevemos este número com o símbolo e no caso do mínimo múltiplo comum de e temos: . Vejamos outro exemplo: Qual é o de e ?
Começamos fazendo uma lista dos múltiplos destes dois números. Na imagem abaixo podemos ver.
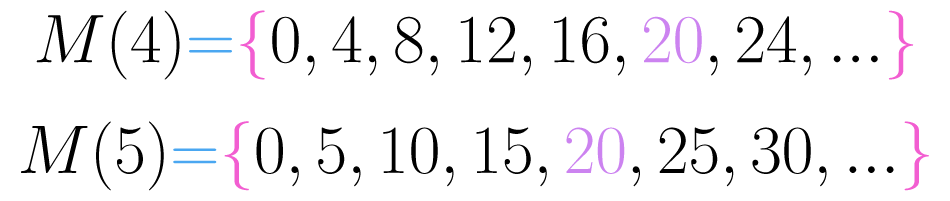
Com base nestes conjuntos de múltiplos podemos observar que o menor dos comuns é . Concluímos que mínimo múltiplo comum de e é : .
/pt/multiplos-e-divisores/como-tirar-o-minimo-multiplo-comum/content/
