/pt/multiplos-e-divisores/problemas-que-podem-ser-resolvidos-com-divisores/content/
Quando entendemos o conceito de múltiplos, podemos compreender mais facilmente outros coisas como a Soma de frações por exemplo.
Os múltiplos de um número são todos os resultados possíveis da multiplicação desse número por todos e por cada um dos números naturais. Assim, os múltiplos de três são: o zero, que é o resultado de multiplicar três por zero: ; o três, que é o resultado da multiplicação de três por um: ; o seis que obtemos ao multiplicar três por dois: , etc.
Como você pode imaginar, o conjunto dos múltiplos de um determinado número (com exceção do zero) é infinito, porque existem infinitos naturais para multiplicar.
Escrevemos o conjunto dos múltiplos do número assim . No caso do três temos : . Na imagem a seguir podemos observar outros exemplos.
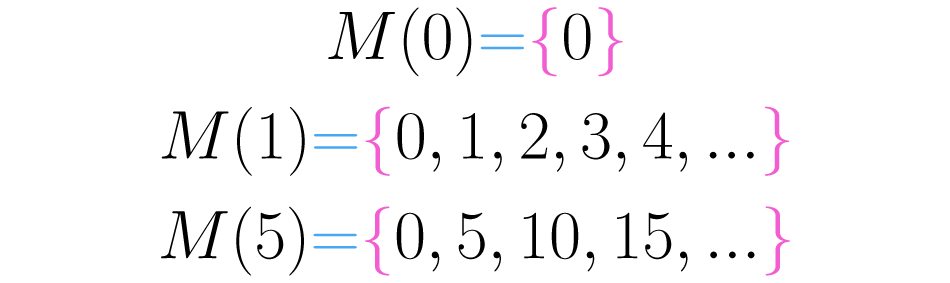
Com base no conceito de múltiplos é possível definir agora um tipo especial de números: os pares. Dizemos que um número é par se ele é múltiplo do dois. Assim, os números , , , , etc., são pares.
Chamamos os números naturais que NÃO são pares de ímpares, assim os números , , , , etc., são impares.
é o conjunto dos pares, e o dos impares, a união é igual ao conjunto de números naturais ou , e sua intersecção é o conjunto vazio.
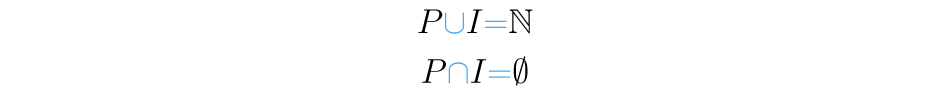
Curiosamente podemos observar que estes dois conjuntos são o resultado de "repartir" o conjunto de números naturais pela "metade". Mas mesmo sendo "metades" de , continuam sendo infinitos. Mas tendo somente a metade de elementos do ,continuam sendo conjuntos infinitos?
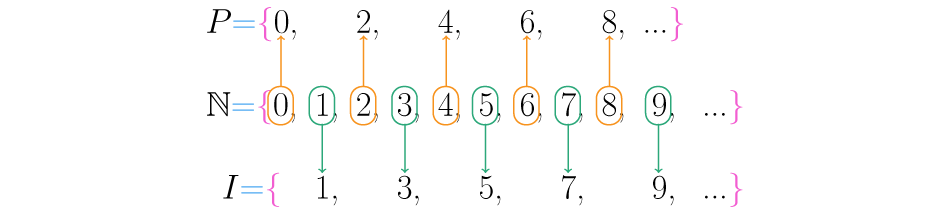
Por incrível que pareça, estes três conjuntos possuem a mesma quantidade de elementos.
/pt/multiplos-e-divisores/o-minimo-multiplo-comum/content/
