Múltiplos e divisores
Os números primos


/pt/multiplos-e-divisores/o-que-sao-divisores/content/
Os números primos desempenham um papel fundamental na matemática. Entenda melhor este importante conceito aqui:
Agora que você conhece o conceito de divisor, poderá entender o que é um número primo. Dizemos que um número natural é primo se ele tem só dois divisores: o um, e ele mesmo.
Com base nisso, dois é primo, porque ; três é primo porque ; cinco é primo, porque . Outros exemplos de números primos são: , etc. Chamamos os números que não são primos de compostos, por exemplo , etc. são números compostos.
O conjunto dos números primos é muito importante, e por isso usamos um símbolo especial para representá-lo, a letra .
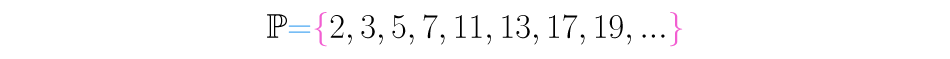
Não existe um padrão para encontrá-los, ou seja, você não poderá encontrá-los contando de dois em dois ou de três em três.
Desde a antiguidade os matemáticos se mostram interessados por este conjunto particular de números. Uma das primeiras perguntas que surgiu sobre eles foi sobre a quantidade existente. Euclides, matemático grego (325-265 a.C.), demonstrou que o conjunto dos números primos é infinito. Significa que não existe um número primo maior que todos os demais, sempre que encontramos um, podemos encontrar um outro maior.
Há vários processos onde é indispensável trabalhar com números primos, por isso precisamos saber como identificá-los. O método que apresentamos abaixo para encontrar números primos é conhecido como Crivo de Eratóstenes, em homenagem ao grande matemático que o criou.
Trata-se de uma tabela onde estão todos os números de um determinado intervalo começando por ele mesmo. A ideia é ir eliminando um a um os números de tal modo que no final só sobrem os primos. Por exemplo, se queremos encontrar os primos do UM até o CEM podemos usar a tabela abaixo.
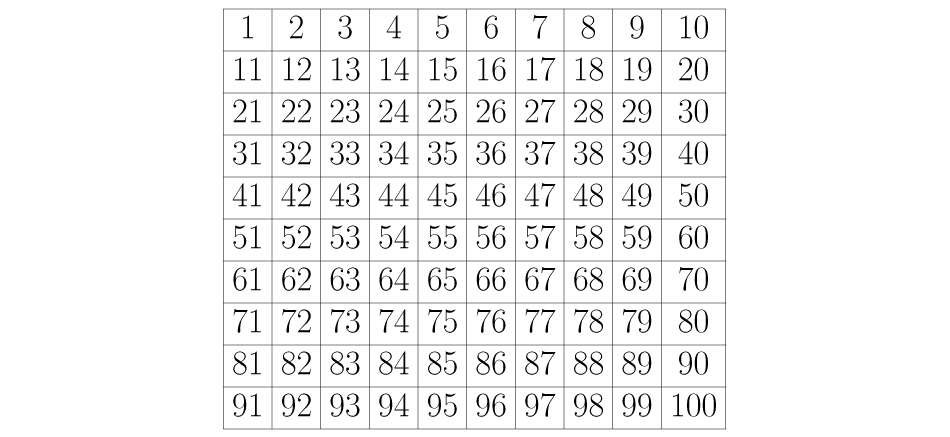
Eliminamos o número da lista porque ele não é um número primo. Seguimos com o número e como ele não foi apagado, o deixamos intacto. Eliminamos todos os números que encontramos contando de dois em dois a partir dele. Isso quer dizer que devemos apagar os números etc.
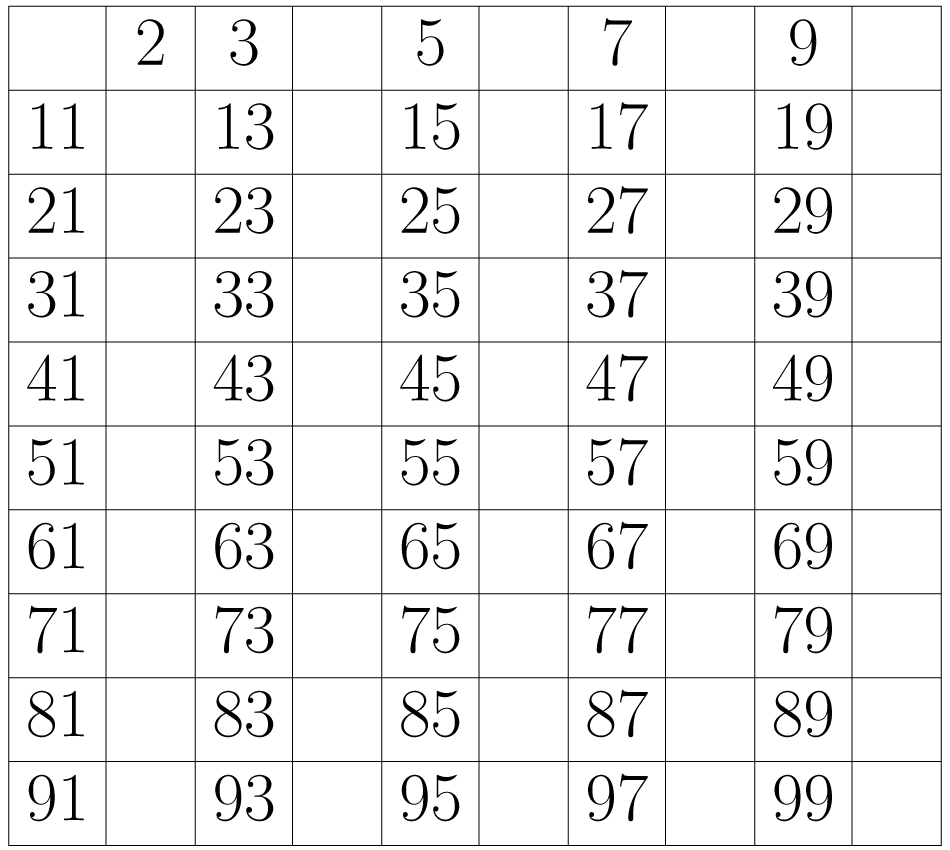
Continuamos com o próximo número que não foi eliminado, ou seja, o três. Como ele não foi apagado, o deixamos na tabela, mas a partir dele eliminamos todos os número que encontramos contando de três em três. Apagamos portanto os números , , , ... etc, e a tabela será reduzida aos números que vemos abaixo:
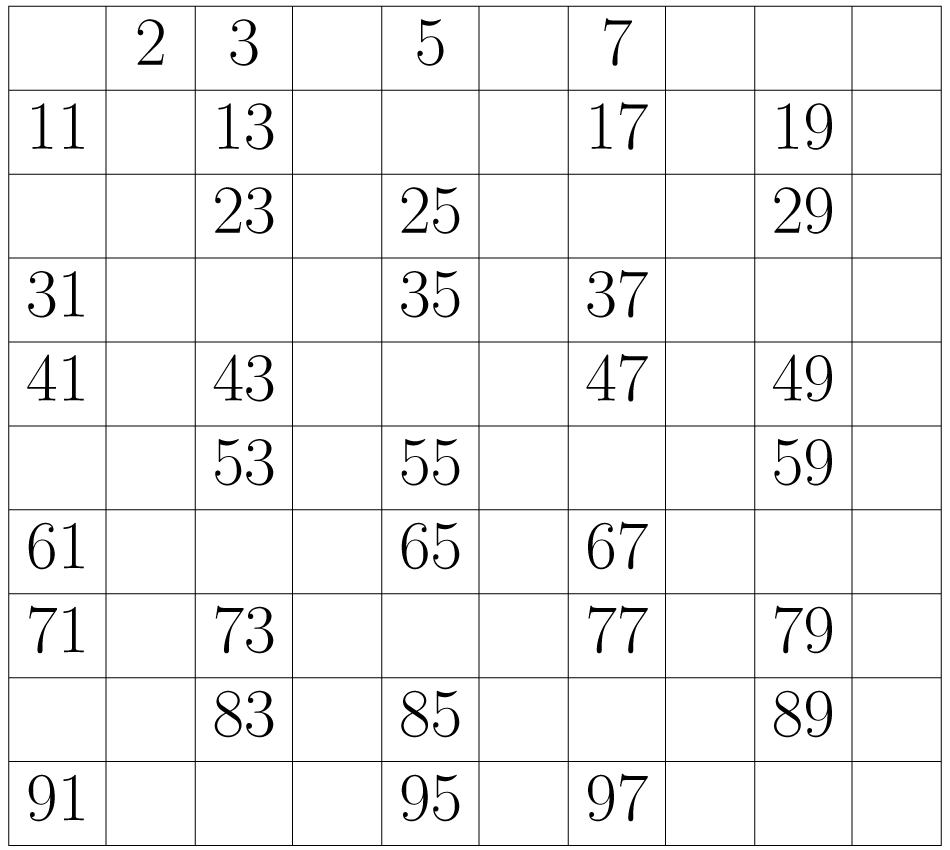
Seguimos o processo com o próximo número sem excluí-lo, o cinco. Ele permanece na tabela, e eliminamos todos os números que encontramos contando de cinco em cinco a partir dele, como vemos na imagem abaixo.
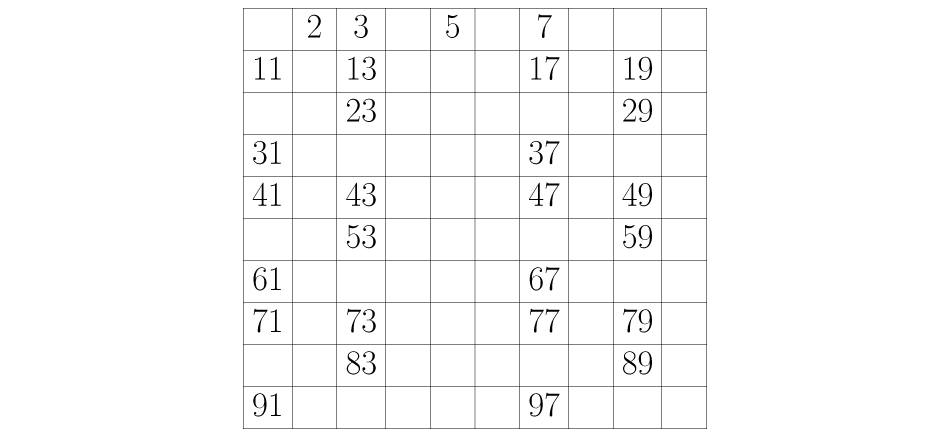
Realizamos o mesmo processo com todos os números que vão ficando na tabela: se um número não foi apagado o deixamos, mas eliminamos os que encontramos contando de um em um conforme o número que estamos trabalhando no momento. Seguindo este procedimento encontraremos todos os números primos que estão entre um e cem:
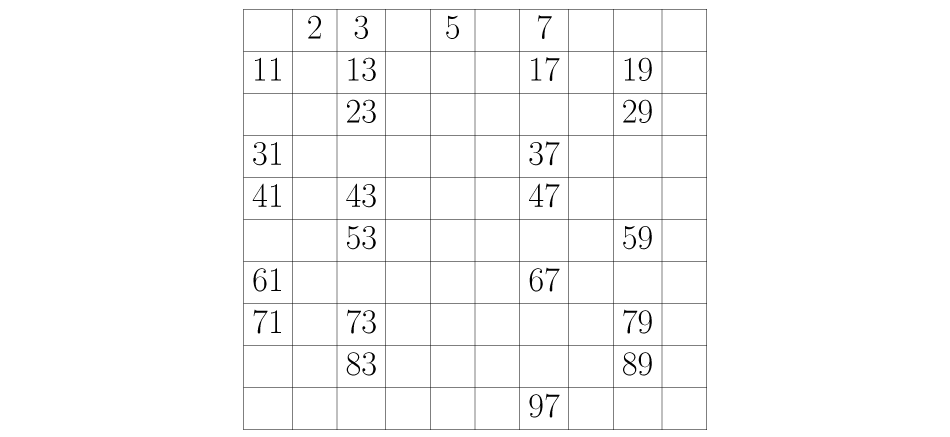
/pt/multiplos-e-divisores/decomposicao-em-fatores-primos/content/