/pt/multiplos-e-divisores/propriedades-do-maximo-divisor-comum/content/
Aprenda a usar o conceito de máximo divisor comum para solucionar problemas. Veja como fazer e depois coloque em prática!
Observe a seguinte situação: um carpinteiro tem dois pedaços de madeira de e centímetros cada um. Ele quer dividi-los em partes iguais com o maior tamanho possível sem que sobre nada. De quantos centímetros deve ser cada uma das partes?
Antes de tentar resolver o problema, vamos analisá-lo um pouco. Suponhamos por exemplo, que ele decide fazer pedaços de centímetros. Quando dividir o pedaço de obterá dois, mas ao dividir o de teria uma parte de centímetros e outra de , que seria desperdiçada porque ele quer que todas as partes sejam iguais.
Para que ele não desperdice nada, a medida das divisões deve ser o divisor comum de e . Além disso, as partes devem ser o maior possível, assim, o divisor que buscamos é o maior; ou seja, o máximo divisor comum. Decompomos os números e para calcular seu
A partir das decomposições e , observamos que os fatores primos comuns (com o menor expoente) são e então o . Concluímos que o carpinteiro deve fazer partes de centímetros.
Observe que o número de bolas em cada caixa deve ser um divisor comum, por exemplo: se empacotamos sete bolas em cada caixa teríamos que usar caixas para as bolas vermelhas e não sobraria nenhuma. Mas para as verdes necessitamos: e sobram , isto quer dizer que ficaria uma caixa com seis bolas verdes. Em contrapartida, se o número de bolas em cada caixa é um divisor comum de e , empacotamos as bolas e não vai sobrar nenhuma.
Sabemos que o número de bolas em cada caixa deve ser o divisor de e de , mas também deve ser o maior possível. Isto é, estamos buscando seu
Como podemos ver na imagem abaixo as decomposições primas são e .
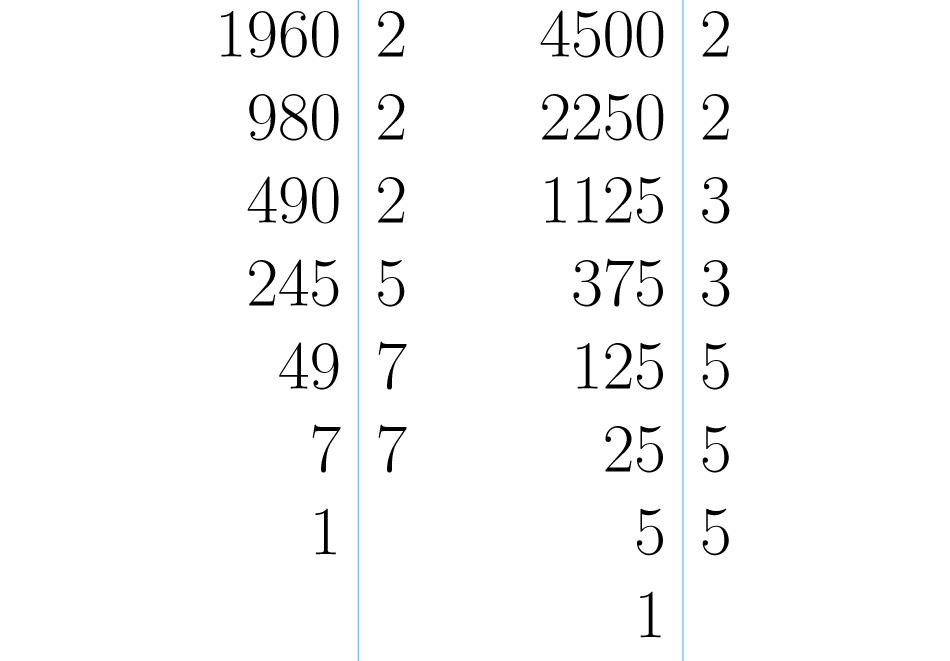
Os fatores primos comuns com menor expoente são e , então . Isto quer dizer que devemos empacotar bolas em cada caixa. Dessa forma asseguramos que haverá o mesmo número em cada uma e também não haverá um número maior que permita uma distribuição sem que sobrem bolas de nenhuma cor.
/pt/multiplos-e-divisores/o-que-sao-multiplos/content/
