/pt/multiplos-e-divisores/propriedades-do-minimo-multiplo-comum/content/
Nesta página veremos exemplos de exercícios resolvidos para praticar os conceitos teóricos que vimos até agora.
Veja o seguinte exemplo: numa estação de ónibus há dois trajetos, o ônibus que faz trajeto passa a cada minutos e o do trajeto a cada . Considerando que os trajetos coincidam em determinado momento, em quantos minutos voltarão a se encontrar na estação?
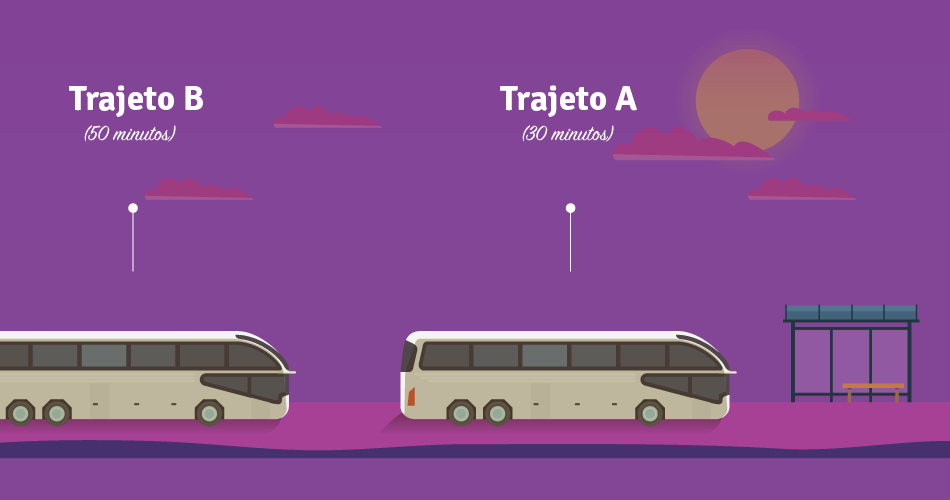
Primeiro analisamos o problema para compreender porque o conceito de múltiplo é adequado para resolvê-lo. Pensemos no ônibus que tem o trajeto e que passa a cada minutos. Observe que a partir de um determinado momento, ele passará aos minutos etc, ou seja, passa nos minutos que são múltiplos de . O mesmo acontece com o que tem o trajeto , que passará nos minutos múltiplos de . Com isso claro, é mais fácil ver que estes trajetos devem se coincidir justamente nos minutos que sejam múltiplos comuns de e .
Para calcular o próximo encontro dos ônibus devemos encontrar o primeiro múltiplo comum diferente de zero, ou seja o mínimo múltiplo comum. Vamos decompor e para poder calcular.
Dois atletas treinam correndo numa pista em e minutos respectivamente. Se eles partem ao mesmo tempo da linha de saída, a cada quanto tempo passam juntos num mesmo ponto?
Fazendo o processo de decomposição percebemos que o de e é o produto . Agora temos certeza que os atletas se encontrarão a cada minutos.
