/pt/multiplos-e-divisores/como-tirar-o-minimo-multiplo-comum/content/
Entenda um pouco mais do conceito de múltiplo através de suas propriedades.
Os conceitos de múltiplo e divisor estão estreitamento ligados. Lembre-se que um número é divisor de outro se estiver contido uma quantidade inteira de vezes nele, por outro lado, um número é múltiplo de outro se o contêm uma quantidade inteira de vezes.
Para que tenhamos uma ideia: exploremos a expressão que deve ser lida como “três vezes cinco é igual a quinze”, ou seja, o cinco está contido três vezes em quinze, e o quinze contêm três vezes o quinze.
Conforme as definições de múltiplo e divisor, podemos dizer que é múltiplo de e ao mesmo tempo é divisor de .
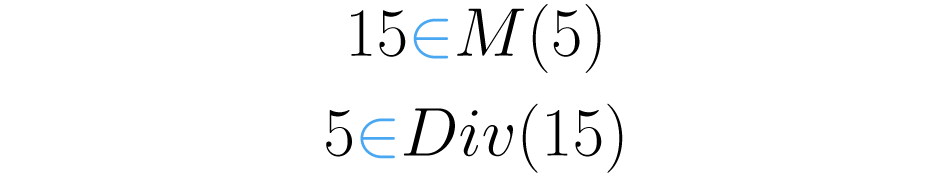
De um modo geral dizemos que se é divisor de , então é múltiplo de .
Como podemos observar, cada vez que calculamos os múltiplos de um certo número, vemos que o próprio número está na lista, por exemplo:
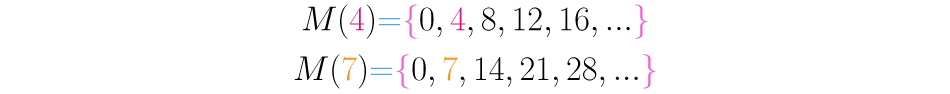
Assim, todo número é múltiplo dele mesmo e usando a linguagem dos conjuntos temos: . Os exemplos anteriores são: e .
Esta propriedade ocorre pelo fato de que todo número multiplicado por zero tem como resultado zero, , portanto será um dos seus múltiplos. Dizemos então que para todo número .
Vejamos esta propriedade através do seguinte exemplo: e são múltiplos de . Quando fazemos a lista dos múltiplos de encontramos que e :
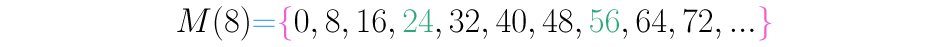
Esta propriedade pode ser lida assim: “se um número é múltiplo de outro, e este de um terceiro, então o primeiro também é múltiplo do terceiro”. Como exemplo, vejamos os números e . é múltiplo de e é múltiplo de , esta propriedade diz que deve ser múltiplo de :
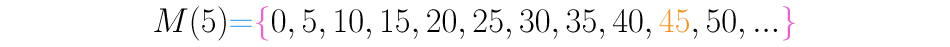
/pt/multiplos-e-divisores/propriedades-do-minimo-multiplo-comum/content/
