/pt/numeros-fracionarios/problemas-com-divisao-de-fracoes/content/

As razões

As Razões são uma das ferramentas básicas mais úteis da matemática. Muitas vezes, sem perceber, as usamos quando estamos preparando uma receita.

A Razão entre duas grandezas é definida como o quociente ou a divisão das mesmas; isto é, dadas as quantidades e , a razão entre elas é , ou o que é igual: . O resultado desta divisão, ou seja, o números , pode ser entendido como as vezes que uma quantidade está na outra. Observe um exemplo: 

Uma receita de arroz diz que a quantidade de água e arroz devem estar na proporção de para . Isso significa que:

Se você quer preparar xícaras de arroz, qual quantidade de água deve ser usada? 

Para responder esta pergunta, note que a razão da receita, dois para um, significa que o número de xícaras de água (numerador) deve ser o dobro da de arroz (denominador). Devemos encontrar um número que quando dividido por três seja equivalente a , e esse número é o seis:

Portanto, seis xícaras de água devem ser usadas e assim teremos a razão: duas xícaras de água para cada uma de arroz. 

Outro exemplo:

Numa empresa química é produzida uma mistura composta pelas substâncias e , com a proporção de . Se são utilizados quilos de substância , quantos quilos de substância  são necessários para que a mistura mantenha a mesma proporção que a fórmula original?

Dizer que as substâncias e devem estar na proporção de para , é equivalente a que, para cada três partes de , deve haver duas partes de Assim, consideramos que os quilos que são usados da substância são aquelas duas partes, das quais se deduz que cada parte é de unidades.

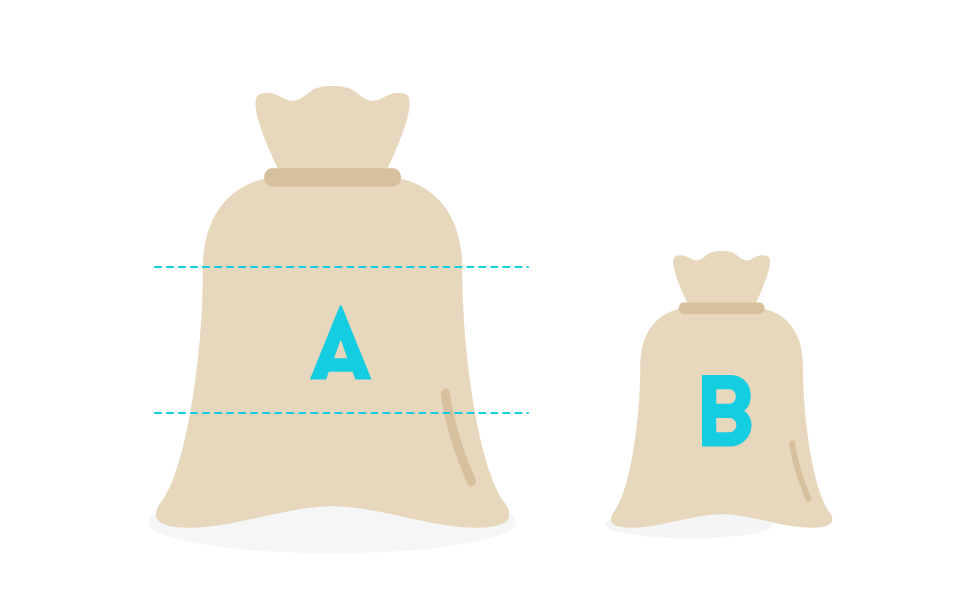
Como cada parte é de quilos, e da substância devemos ter três partes, percebemos que deve ser usado quilos de substância . É fácil verificar que nossa resposta está correta porque a Razão de e é igual à razão entre e e quando as Razões são preservadas temos frações equivalentes:

Os usos das Razões vão além desses exemplos simples: As Razões trigonométricas, conceitos físicos como a densidade, a corrente ou a definição do número são alguns outros.

/pt/numeros-fracionarios/as-taxas/content/