/pt/numeros-fracionarios/problemas-com-multiplicacao-de-fracoes/content/
Ainda nos falta aprender uma operação com frações: a divisão. Veja as diferentes formas de fazê-la:
Você já sabe que a expressão é outra maneira de representar a operação .Desta forma, quando você está trabalhando com uma divisão pode interpretá-la assim:
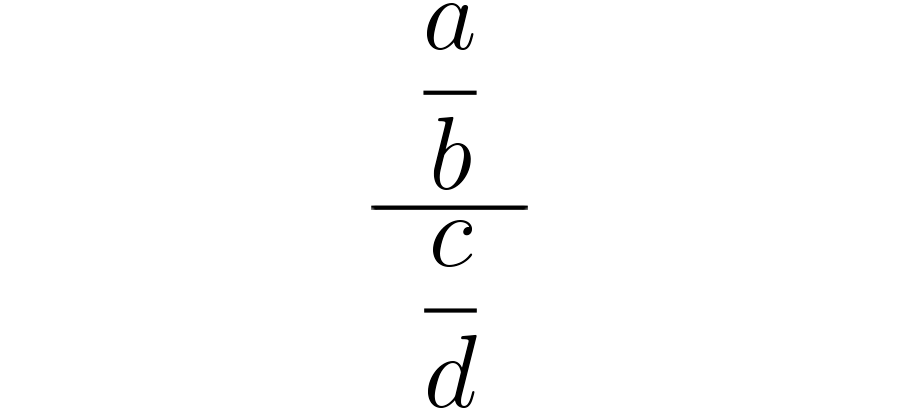
Este procedimento indica que as extremidades superior e inferior são multiplicadas para obter o numerador e os números do meio para obter o denominador.
Na imagem abaixo você pode ver como é feito:
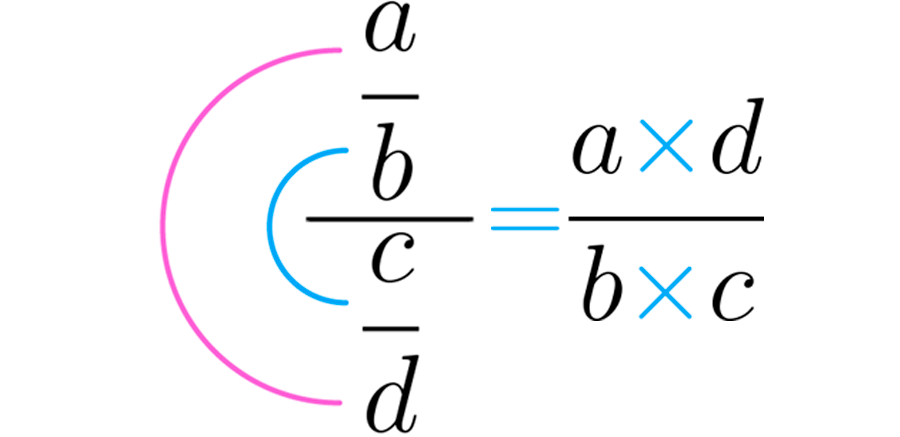
Agora vamos usar esse método para executar a divisão
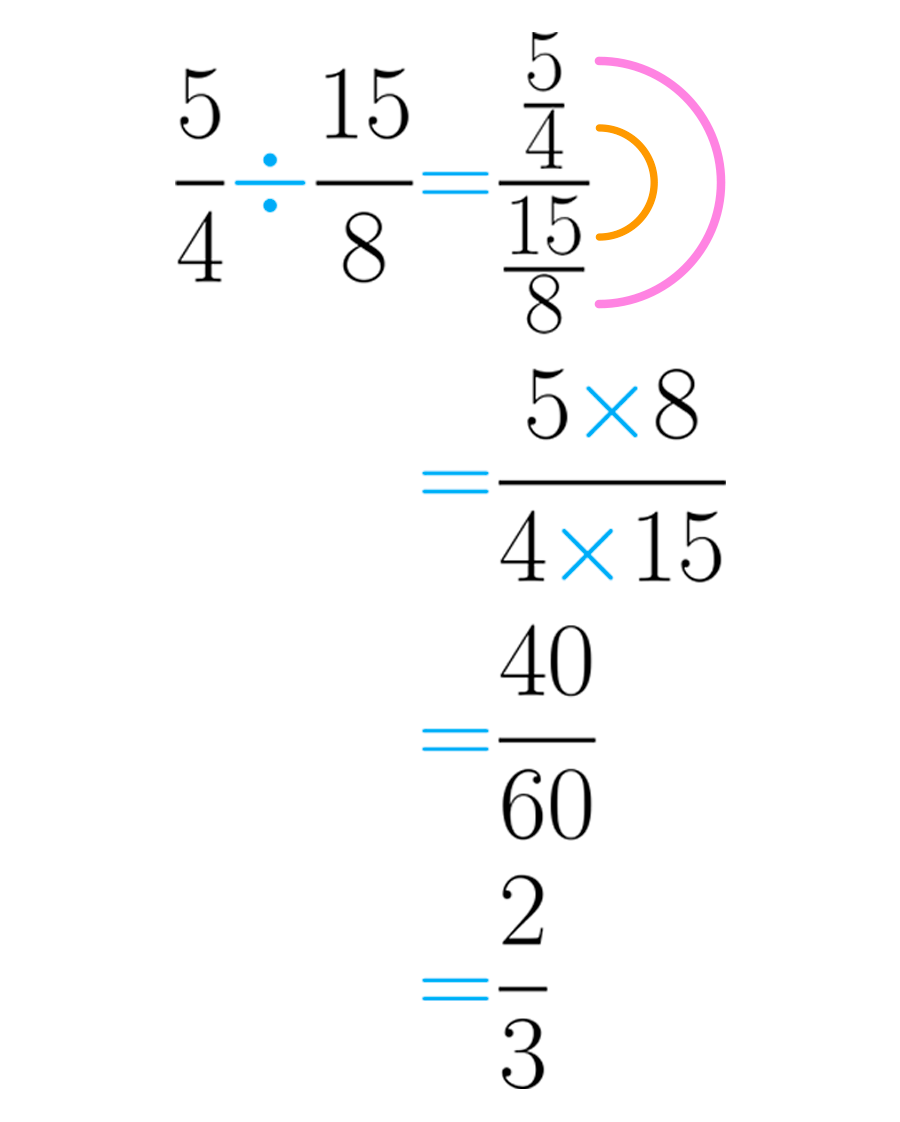
Você pode ver que é chamado de "orelha", porque se perece precisamente com esta parte do nosso corpo.
O resultado da divisão é , no entanto, depois de simplificar esta expressão, obtemos a fração , que é irredutível.
Existe outra maneira de dividir as frações: os "produtos cruzados". Com este método, não é necessário colocar as frações uma em cima da outra, simplesmente multiplicamos o numerador pelo denominador e o denominador pelo numerador. Observe este exemplo:
Realizamos a operação :
Primeiro multiplicamos o numerador do dividendo pelo denominador do divisor. Este será o numerador da resposta. Em seguida, multiplicamos o denominador do dividendo pelo numerador do divisor. Esse resultado será o denominador do quociente:
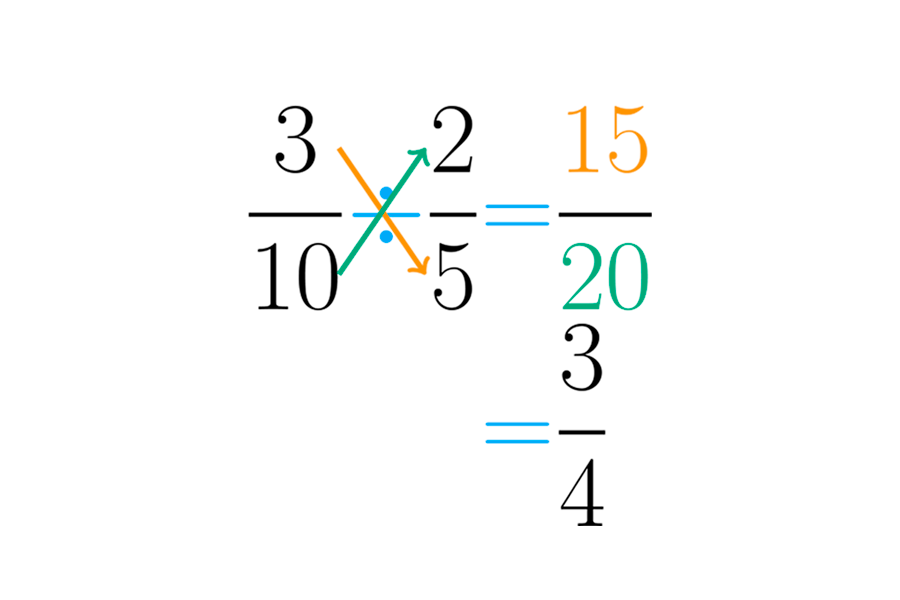
Podemos observar assim que os resultados obtidos pela "regra da orelha" e "pelos "produtos cruzados" sempre serão os mesmos.
/pt/numeros-fracionarios/problemas-com-divisao-de-fracoes/content/
