Números Fracionários
Frações equivalentes


/pt/numeros-fracionarios/fracoes-negativas/content/
O conceito de fração equivalente é indispensável para adicionar ou subtrair frações. Se você quiser entender bem o mundo das frações, é importante conhecê-lo.
Analisamos a seguinte situação: Bete e Diego estão numa pista de corrida de metros de comprimento. Bete diz para Diego que ela corre mais do que ele, porque pode correr dois sextos da pista sem parar. No entanto, Diego responde que isso não é verdade porque ele pode correr um terço da pista sem parar. Qual dos dois está certo?
Para responder a esta pergunta devemos calcular com precisão quantos metros cada um corre, começamos com Bete:
Como ela corre da pista, devemos dividir o comprimento total da pista em seis: e assim sabemos que cada uma das seis partes mede metros. O dois na operação indica que ela corre duas dessas seis partes: portanto, Bete consegue correr metros sem parar.
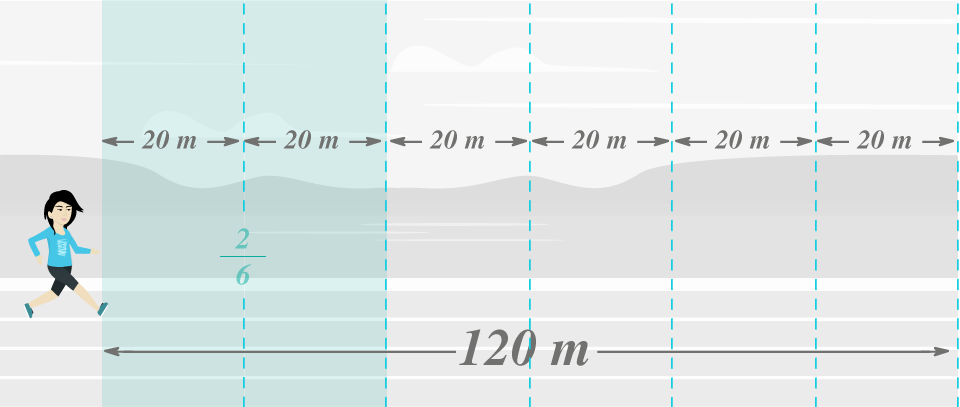
Diego corre um terço, assim devemos dividir o comprimento da pista em três partes. Fazemos a divisão O um da fração indica que corre apenas uma dessas partes, então sabemos que corre metros:
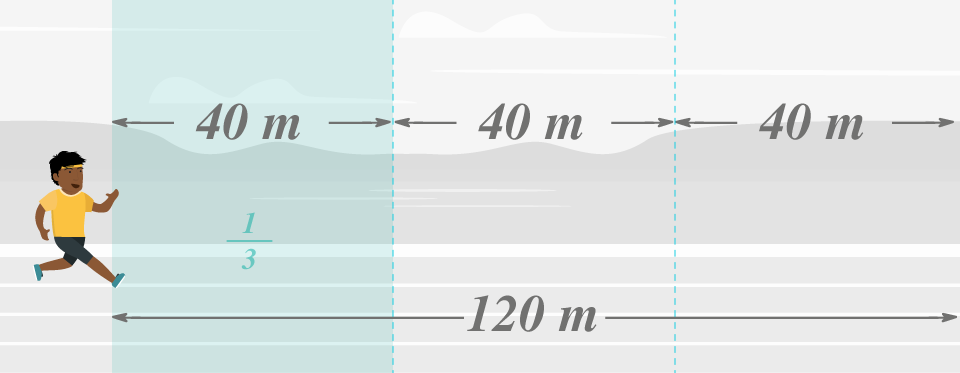
Embora as distâncias percorridas por Bete e Diego sejam representadas por diferentes frações, elas são as mesmas. Por isso dizemos que as frações e são equivalentes, pois representam a mesma quantidade. Por isso escrevemos . No interativo abaixo você pode observar uma demonstração do que acabamos de dizer.
É importante saber quando duas frações são equivalentes, e há uma maneira fácil de verificar isso. Vejamos:
Dadas as frações e,se os produtos e forem iguais, as frações são equivalentes.
Ou seja, devemos multiplicar "em cruz", como mostrado na imagem a seguir.
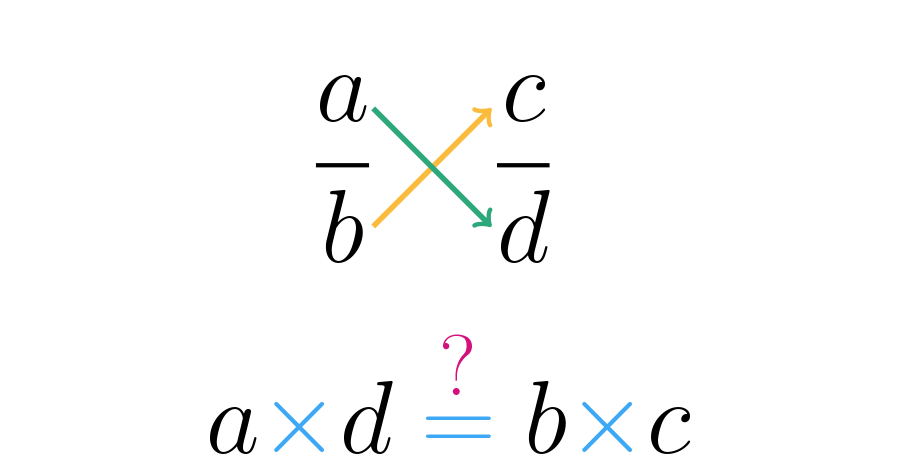
Lembre-se de que esse esquema é o mesmo que fazemos para determinar quando uma fração é maior do que outra.
Observe: as frações e são equivalentes? Como podemos afirmar que sim.
Vejamos outro exemplo: as frações e são equivalentes? Ou seja, elas representam a mesma quantidade?
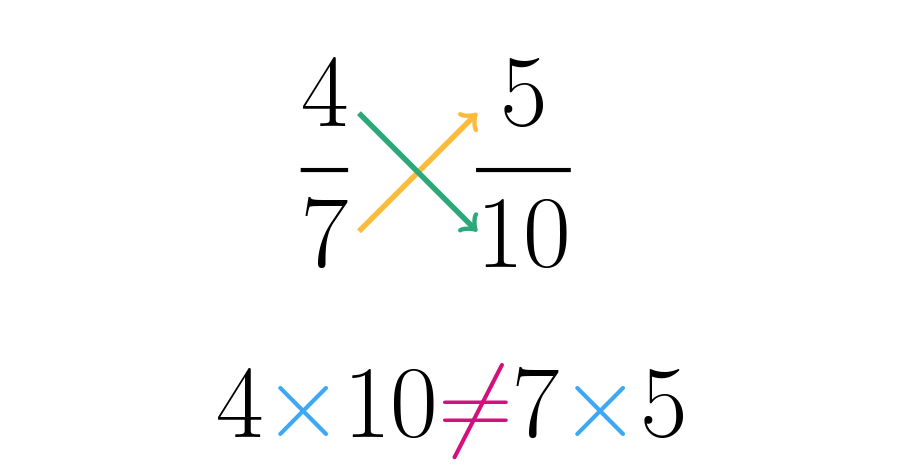
Como os resultados das multiplicações não são iguais, dizemos que não são equivalentes.
Neste caso, escrevemos , pois estas duas frações não representam a mesma quantidade.
/pt/numeros-fracionarios/fracoes-equivalentes-para-inteiros-e-naturais/content/