Números Fracionários
Soma de frações homogêneas


/pt/numeros-fracionarios/numeros-mistos/content/
É comum que a adição e a subtração de frações sejam ensinadas através de fórmulas que temos que decorar. Aqui nesta página, você entenderá porquê e assim nunca mais esquecerá!
O segredo para aprender a fazer adição e subtração de frações é entender a linguagem usada para representá-las. Começamos somando frações com o mesmo denominador, por exemplo .
Quando duas ou mais frações possuem o mesmo denominador, elas são consideradas homogêneas.
Primeiro é necessário responder a seguinte pergunta: Quantos terços a expressão representa?
Se você consegue responder rapidamente, é sinal de que já está entendendo a linguagem das frações. A resposta está na forma como lemos a expressão , que é dois terços.
Se usarmos círculos para representar unidades, podemos interpretar cada terço como mostra o interativo abaixo.
Mova o cursor sobre a barra horizontal que está embaixo do círculo para poder observar como obtemos essa fração.
Podemos entender a expressão dois terços, , como mostra a imagem abaixo:

Como você pode observar, são separadas duas partes e cada uma delas é o resultado da divisão da unidade por três (o círculo). Depois que entendemos isso, fica muito mais fácil adicionar frações que tenham o mesmo denominador: Agora observe como fazemos a soma .
Mas antes vamos pensar na seguinte situação: quantos são cinco lápis mais seis lápis? Simples: onze lápis. Como estamos adicionando objetos iguais, apenas somamos as quantidades. Se você trocar o tipo de objeto, o raciocínio será o mesmo: quantos são cinco tomates mais seis tomates? Onze tomates.
Devemos usar a mesma lógica com as frações homogêneas: quando interpretamos a expressão , podemos visualizar cinco objetos do mesmo tipo: cinco terços. Da mesma forma a expressão representa seis objetos do mesmo tipo: seis terços. Na imagem abaixo podemos ver uma interpretação gráfica desta soma:
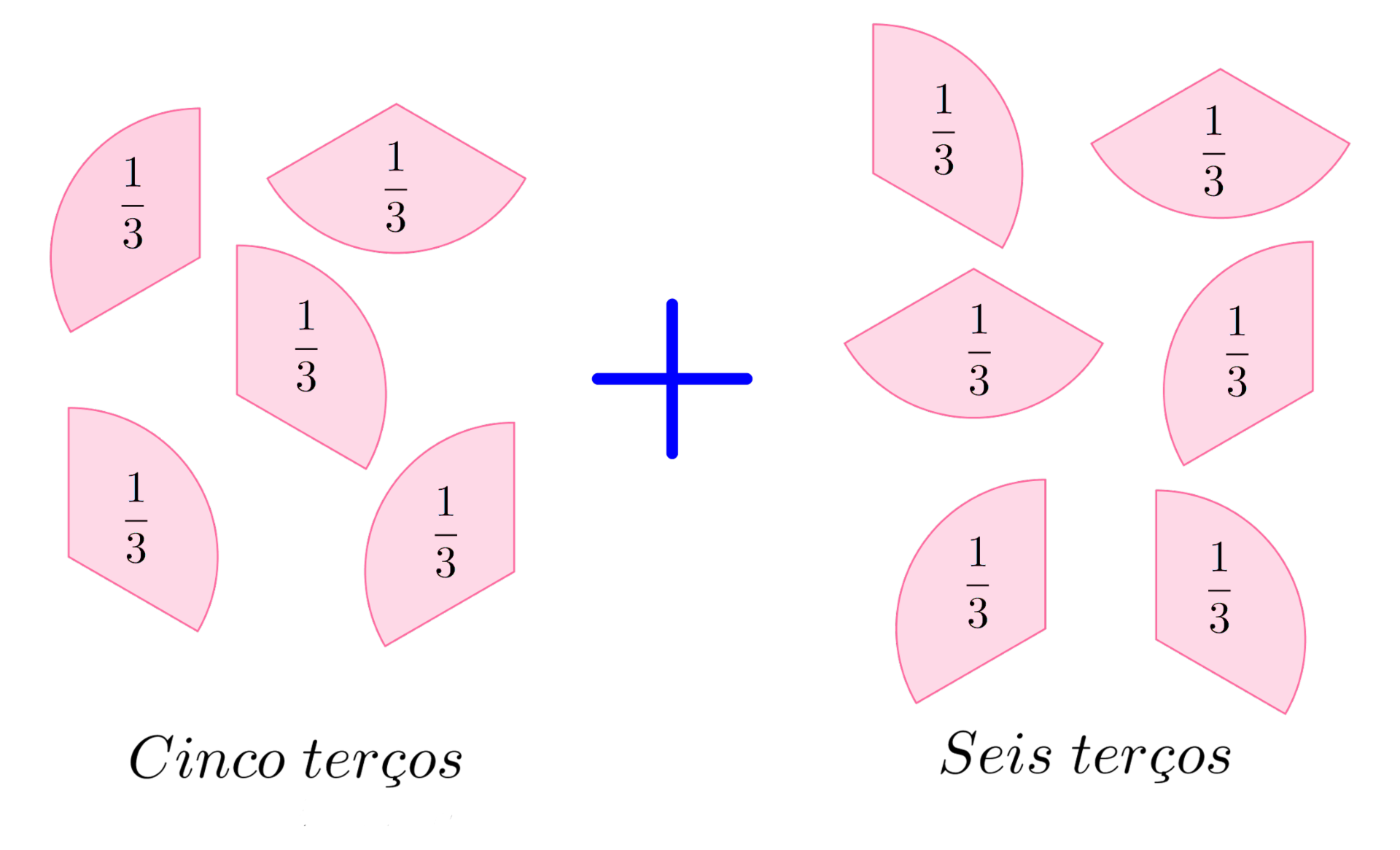
Quando fazemos uma simples contagem de todos os terços, podemos dizer que há onze terços. Assim:
Observe que o denominador da resposta é igual ao denominador das parcelas, e o numerador é a soma dos numeradores. Por este motivo, usamos a seguinte fórmula:
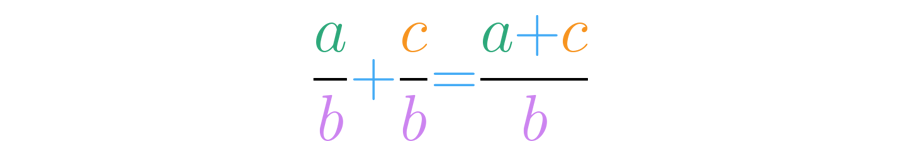
Agora fica claro que você não precisará mais decorar porque adicionar frações homogêneas é tão fácil como somar lápis, tomates ou qualquer outro tipo de objeto.
/pt/numeros-fracionarios/soma-de-fracoes-heterogeneas/content/