Os números decimais
Converter dízimas periódicas compostas em fração


/pt/os-numeros-decimais/converter-dizimas-periodicas-simples-em-fracao/content/
Talvez este método pareça um pouco complicado, mas é muito eficaz. Certamente, quando você aprender mais conceitos matemáticos, entenderá porque isso acontece. Neste momento recomendamos praticar o máximo que puder.
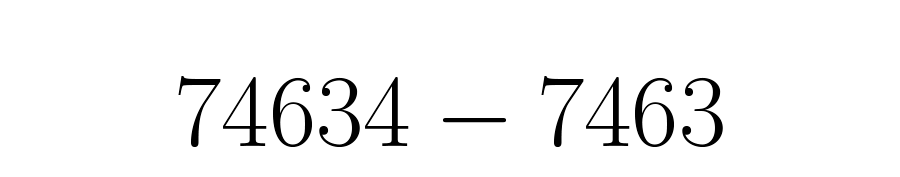
O denominador terá a mesma quantidade de noves que tem a parte que se repete periodicamente, seguidos pela mesma quantidade de zeros da parte decimal que não se repete.
Neste caso há apenas um dígito que é repetido periodicamente, o , portanto, haverá apenas um nove. A parte decimal que não se repete tem dois dígitos: o e o portanto depois do nove vai dois zeros.
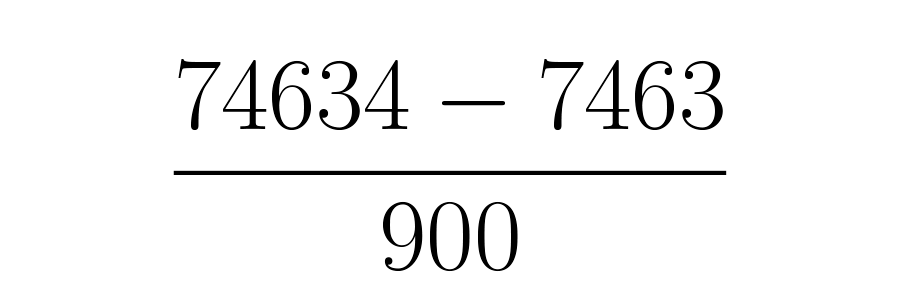
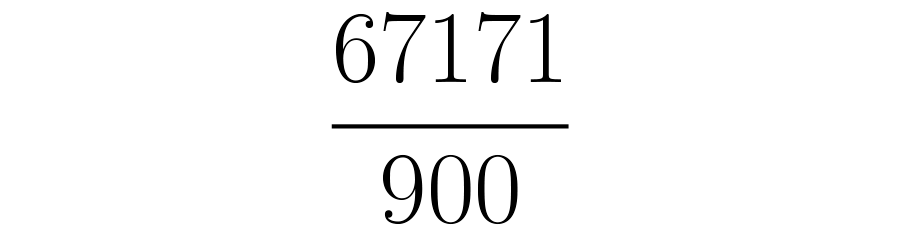
O resultado acima significa que . Se você quiser ter certeza desse resultado, basta fazer a divisão , e vai ver que o resulta dá
O numerador será o decimal completo: menos aparte inteira seguida pela parte decimal que não se repete: . Tudo escrito sem vírgulas ou barras:
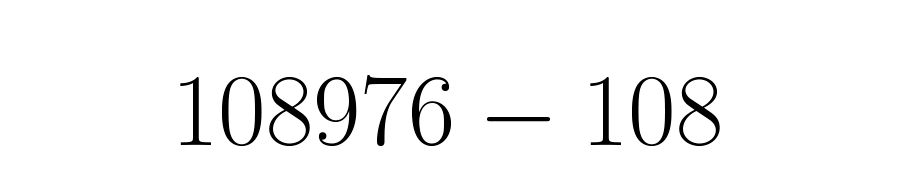
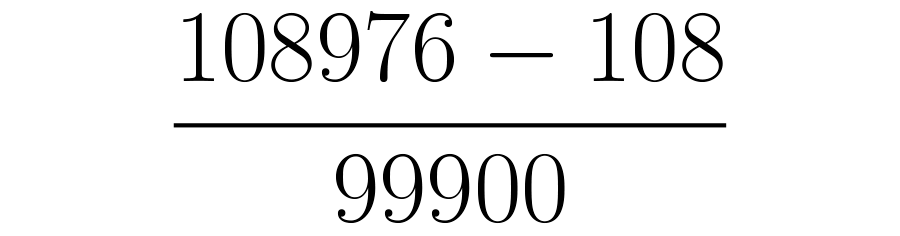
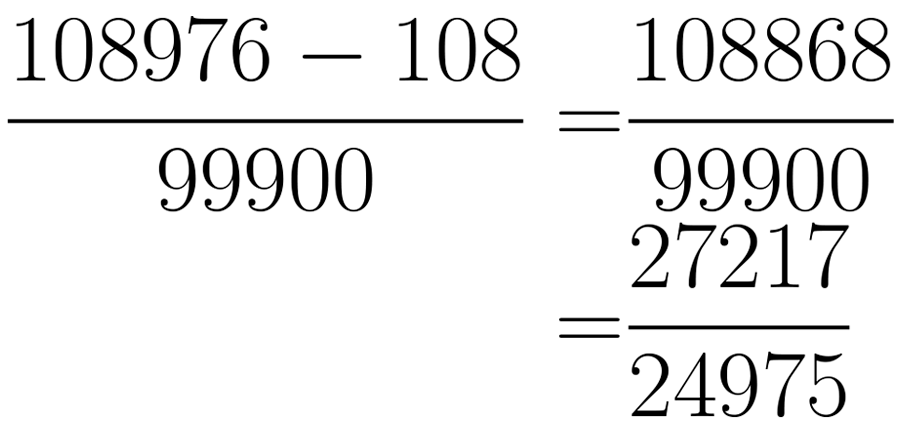
/pt/os-numeros-decimais/converter-decimais-infinitos-nao-periodicos-em-fracao/content/