Usando a matemática
A coroa do rei e a banheira de Arquimedes


/pt/usando-a-matematica/as-coordenadas-geograficas/content/
Talvez em algumas ocasiões, você já pensou em comprar uma jóia de ouro para dar de presente à alguém ou para você mesmo. Brincos, correntes, anéis ou colares são alguns dos objetos mais desejados por algumas pessoas. Se você não é um especialista em jóias, é possível que não consiga saber se um objeto é de ouro ou se está sendo enganado. Não é difícil encontrar algum comerciante desonestos que queira passar a perna em pessoas que não conhecem muito bem o assunto.
A história conta que há muito tempo um rei mandou fazer uma coroa de ouro e teve a mesma dúvida, mas graças à habilidade de um grande pensador, foi capaz de saber se estava sendo enganado ou não. É possível que quando você conheça o método usado para decifrar a situação, não caia no conto do vigário.
O Rei Hierão II (306-215 A.C.),de Siracusa, deu uma certa quantidade de ouro para que lhe fabricassem uma coroa. O material foi enviado para um renomado ourives, a quem ele pediu para fabricá-la sem misturar outros materiais, nem mesmo pedras preciosas como diamantes ou rubis. Mais tarde, o artesão entregou ao rei uma peça fantástica, uma bela coroa digna do mais alto louvor. O rei gostou da coroa, mas suspeitou que a coroa não foi feita com todo o ouro que ele havia dado para sua fabricação. Talvez o artesão tivesse misturado o ouro com outros materiais para roubar uma parte do metal precioso.
Naquela época vivia em Siracusa um dos homens mais inteligentes da história da humanidade: Arquimedes. Este personagem foi designada para a difícil tarefa de demonstrar se a coroa era de ouro puro ou se o ourives tinha enganado o rei. Arquimedes devia que encontrar uma solução sem danificar a jóia tão cara.
Para entender qual foi a solução encontrada por Arquimedes, devemos primeiro compreender alguns conceitos:
Enquanto a massa e o volume são características físicas próprias de um corpo em particular, a densidade é uma medida que relaciona estes dois. Para poder calcular temos que dividir a massa corporal pelo seu volume. Por exemplo, se um corpo tem uma massa de kg e um volume de metros cúbicos, a sua densidade será de quilos por metro cúbico:
Este conceito nos dá uma ideia sobre a concentração de matéria que tem um corpo por unidade de volume. O interessante é que cada elemento tem sua densidade específica, ou seja, não importa de que quantidade de massa estamos falando, se for o mesmo material, sempre que dividirmos sua massa pelo seu volume teremos o mesmo resultado. Tomemos como exemplo a densidade da água numa temperatura normal: centímetros cúbicos pesam gramas, enquanto que centímetros cúbicos pesam gramas. Se calculamos a densidade teremos:
e
Ou seja, a densidade da água em temperatura ambiente é de . Como você pode ver a densidade não foi alterada.O mesmo acontece com os diferentes materiais, como o ouro por exemplo.
Continuando a história, um dia Arquimedes, que ficou um longo tempo sem resolver o problema, decidiu tomar um banho. Quando ele mergulhou o corpo na água, percebeu que a água se descolava, inclusive uma parte dela transbordou para fora da banheira que ele estava. Percebendo isso, Arquimedes pensou que o volume de água que deslocou é igual ao volume do corpo que é mergulhado nela. Ali estava a solução, na água! Dizem que foi tanta sua emoção que imediatamente saiu correndo pelado pelas ruas e gritando aos quatro ventos!, Eureka!, Encontrei, Encontrei
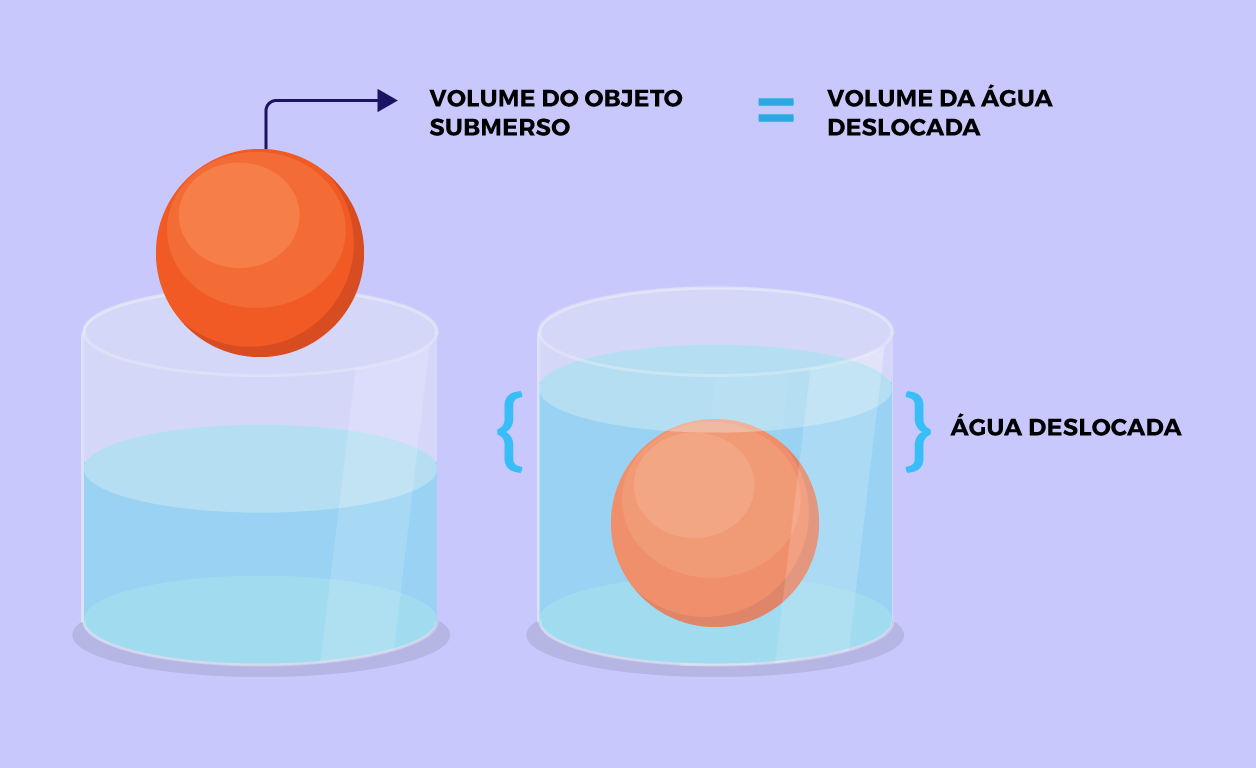
Graças à descoberta de Arquimedes, o problema da coroa ficou mais fácil de ser resolvido, pois tinha encontrado uma maneira de medir seu volume. Bastava mergulhar a coroa e medir o volume de água que se movia, este volume deveria ser igual ao volume da coroa. Sabendo qual era sua massa e volume ele poderia calcular a sua densidade e, portanto, verificar se era ou não ouro puro. Esta descoberta o conduziu a um novo conceito da física.
Nosso amigo perspicaz também descobriu que a água deslocada faz uma força para cima do objetos que estão mergulhados nela, e por este motivo, quando levantamos algo debaixo d'água ele fica muito mais leve. Esta força depende diretamente do volume de água que se desloca: quanto mais volume de água se desloca, mais força ao empurrar para cima sofre o corpo submerso. Este fenômeno físico é conhecido como o princípio de Arquimedes.

Mas como foi possível usar o princípio de Arquimedes para saber se a coroa estava feita totalmente de ouro?
Em um dos pratos de uma balança, foi posto uma quantidade de ouro que pesa exatamente a mesma que o rei entregou para o artesão, e no outro a coroa. Agora pense nisso: o ouro entregue pelo rei para a confecção da coroa ocupa um certo volume, e isso não mudou quando ele foi moldado em coroa, se a coroa não tem alterações deve ter o mesmo volume de ouro entregue para sua criação. Inversamente, se a coroa tivesse sido alterada com outro material como o cobre, o seu volume será maior, pois para preservar o peso original se deve usar uma quantidade de cobre que coincidisse com o peso de ouro roubado, e como o cobre é menos denso que o ouro se deveria ser usar um volume maior.
Assim, no ar, a coroa e o ouro têm o mesmo peso; mas se submersa na água, a coroa alterada sofrerá mais força ao ser empurrada para cima pois seu volume será maior e deslocará mais água. Portanto, a balança ficará inclinada como mostramos na animação abaixo:

Arquimedes era um homem brilhante, e devemos à sua descoberta, incontáveis contribuições para a matemática, como a engrenagem e muitos outros, sobre a qual Arquimedes disse:"Dê-me um ponto de apoio e eu moverei o mundo".
Infelizmente Arquimedes foi assassinado por um soldado quando o exército romano, comandado pelo general Marcelo estava roubando Siracusa. Marcelo deu ordens estritas para não prejudicarem o personagem tão ilustre mas quando um soldado romano o encontrou concentrada em um problema geométrico o levou para o general. Arquimedes ignorou a situação e o soldado e ele lhe enfiou a espada. As últimas palavras de Arquimedes foram: "Não toquem nos meus círculos".
/pt/usando-a-matematica/por-que-existem-as-estacoes-do-ano/content/